
 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.
如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.分析 (1)根据正弦的定义求出AD,根据直角三角形的性质求出AC即可;
(2)利用余弦的概念分别求出BD、CD,计算即可.
解答 解:(1)在Rt△ABD中,AD=ABSin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
在Rt△ABD中,∠ACD=30°,
∴AC=2AD=4$\sqrt{2}$≈5.64,
答:新传送带AC的长度约为5.64m;
(2)在Rt△ABD中,BD=ABcos45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
在Rt△ACD中,CD=ABcos30°=4$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=2$\sqrt{6}$,
∴CB=CD-BD=2$\sqrt{6}$-2$\sqrt{2}$≈2.08,
∵PC=PB-CB≈4-2.08=1.92<2,
∴货物MNQP需要挪走.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调入地 水量/万吨 调出地 | C | D |
| A | x | 200-x |
| B | 240-x | 60+x |
| 总计 | 240 | 260 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
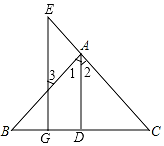 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
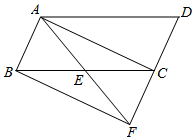 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.
如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F,且AF=AD,连接BF,求证:四边形ABFC是矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com