
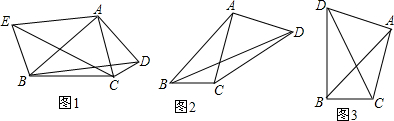
·ÖĪö £Ø1£©Ź×ĻČøł¾ŻµČŹ½µÄŠŌÖŹÖ¤Ć÷”ĻEAC=”ĻBAD£¬Ōņøł¾ŻSAS¼“æÉÖ¤Ć÷”÷EAC”Õ”÷BAD£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æÉÖ¤Ć÷£»
£Ø2£©ŌŚ”÷ABCµÄĶā²æ£¬ŅŌAĪŖÖ±½Ē¶„µć×÷µČŃüÖ±½Ē”÷BAE£¬Ź¹”ĻBAE=90”ć£¬AE=AB£¬Į¬½ÓEA”¢EB”¢EC£¬Ö¤Ć÷”÷EAC”Õ”÷BAD£¬Ö¤Ć÷BD=CE£¬Č»ŗóŌŚÖ±½ĒČż½ĒŠĪBCEÖŠĄūÓĆ¹“¹É¶ØĄķ¼“æÉĒó½ā£»
£Ø3£©ŌŚĻ߶ĪACµÄÓŅ²ą¹żµćA×÷AE”ĶABÓŚµćA£¬½»BCµÄŃÓ³¤ĻßÓŚµćE£¬Ö¤Ć÷”÷EAC”Õ”÷BAD£¬Ö¤Ć÷BD=CE£¬¼“æÉĒó½ā£®
½ā“š ½ā£ŗ£Ø1£©BD=CE£®
ĄķÓÉŹĒ£ŗ”ß”ĻBAE=”ĻCAD£¬
”ą”ĻBAE+”ĻBAC=”ĻCAD+”ĻBAC£¬¼“”ĻEAC=”ĻBAD£¬
ŌŚ”÷EACŗĶ”÷BADÖŠ£¬
$\left\{\begin{array}{l}{AE=AB}\\{”ĻEAC=”ĻBAD}\\{AC=AD}\end{array}\right.$£¬
”ą”÷EAC”Õ”÷BAD£¬
”ąBD=CE£»
£Ø2£©ČēĶ¼2£¬ŌŚ”÷ABCµÄĶā²æ£¬ŅŌAĪŖÖ±½Ē¶„µć×÷µČŃüÖ±½Ē”÷BAE£¬Ź¹”ĻBAE=90”ć£¬AE=AB£¬Į¬½ÓEA”¢EB”¢EC£®
”ß”ĻACD=”ĻADC=45”ć£¬
”ąAC=AD£¬”ĻCAD=90”ć£¬
”ą”ĻBAE+”ĻBAC=”ĻCAD+”ĻBAC£¬¼“”ĻEAC=”ĻBAD£¬
ŌŚ”÷EACŗĶ”÷BADÖŠ£¬
$\left\{\begin{array}{l}{AE=AB}\\{”ĻEAC=”ĻBAD}\\{AC=AD}\end{array}\right.$£¬
”ą”÷EAC”Õ”÷BAD£¬
”ąBD=CE£®
”ßAE=AB=5£¬
”ąBE=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$£¬”ĻABE=”ĻAEB=45”ć£¬
Ó֔ߔĻABC=45”ć£¬
”ą”ĻABC+”ĻABE=45”ć+45”ć=90”ć£¬
”ąEC=$\sqrt{E{B}^{2}+B{C}^{2}}$=3$\sqrt{6}$£¬
”ąBD=CE=3$\sqrt{6}$£®
£Ø3£©ČēĶ¼3£¬ŌŚĻ߶ĪACµÄÓŅ²ą¹żµćA×÷AE”ĶABÓŚµćA£¬½»BCµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓBE£®
”ßAE”ĶAB£¬
”ą”ĻBAE=90”ć£¬
Ó֔ߔĻABC=45”ć£¬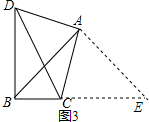
”ą”ĻE=”ĻABC=45”ć£¬
”ąAE=AB=5£¬BE=5$\sqrt{2}$£¬
Ó֔ߔĻACD=”ĻADC=45”ć£¬
”ą”ĻBAE=”ĻDAC=90”ć£¬
”ą”ĻBAE-”ĻBAC=”ĻDAC-”ĻBAC£¬¼“”ĻEAC=”ĻBAD£¬
ŌŚ”÷EACŗĶ”÷BADÖŠ£¬
$\left\{\begin{array}{l}{AE=AB}\\{”ĻEAC=”ĻBAD}\\{AC=AD}\end{array}\right.$£¬
”ą”÷EAC”Õ”÷BAD£¬
”ąBD=CE£¬
”ßBC=2£¬
”ąBD=CE=£Ø5$\sqrt{2}$-2£©cm£®
µćĘĄ ±¾Ģāæ¼²éČ«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ”¢¹“¹É¶ØĄķµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĄķ½āĢāŅā£¬ÕżČ·Ń°ÕŅČ«µČČż½ĒŠĪ½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼³£æ¼ĢāŠĶ£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2 | B£® | 1 | C£® | 0 | D£® | -3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2a+3b=5ab | B£® | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C£® | £Øa+b£©2=a2+b2 | D£® | a6”Āa3=a2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
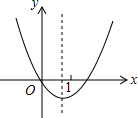 ŅŃÖŖÅ×ĪļĻßy=ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬Ōņ|b-a-2c|+|3a+b|=£Ø””””£©
ŅŃÖŖÅ×ĪļĻßy=ax2+bx+cµÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬Ōņ|b-a-2c|+|3a+b|=£Ø””””£©| A£® | 2a+2b | B£® | -2a-2b | C£® | -4a-2b | D£® | 4a |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | $\frac{1}{3}$ | B£® | $\sqrt{2}$ | C£® | 0 | D£® | |-5| |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2 | B£® | -$\frac{1}{2}$ | C£® | 3.14 | D£® | $\sqrt{3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -1 | B£® | 0 | C£® | $\frac{1}{2}$ | D£® | -3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼£¬ŅŃÖŖAB”¢ADŹĒ”ŃOµÄĻŅ£¬”ĻB=20”ć£¬”ĻD=15”ć£¬Ōņ”ĻBADµÄ¶ČŹżŹĒ£Ø””””£©
ČēĶ¼£¬ŅŃÖŖAB”¢ADŹĒ”ŃOµÄĻŅ£¬”ĻB=20”ć£¬”ĻD=15”ć£¬Ōņ”ĻBADµÄ¶ČŹżŹĒ£Ø””””£©| A£® | 30”ć | B£® | 45”ć | C£® | 20”ć | D£® | 35”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com