
【题目】如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:
①∠BAD=2∠F;②∠E+∠F=90°
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:(1)AD∥BC.理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠________,(________)
∴AD∥BC
(2)AB与EF的位置关系是:________.
∵BE平分∠ABC,(已知)
∴∠ABE=![]() ∠ABC.(角平分线的定义)
∠ABC.(角平分线的定义)
又∵∠ABC=2∠E,(已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠________.(________)
∴________∥________.(________)

【答案】(1)BCF,同角的补角相等;(2)AB∥EF,ABE,等量代换,AB,EF,内错角相等,两直线平行;(3)①证明见解析;②证明见解析
【解析】
(1)欲证明AD∥BC,只要证明∠ADF=∠BCF即可;
(2)结论:AB∥EF,只要证明∠E=∠ABE 即可;
(3)①根据平行线的性质以及角平分线的定义即可证明;
②只要证明∠OAB+∠OBA=90°即可解决问题;
(1)解:结论:AD∥BC.理由如下:
∵∠ADE+∠ADF=180°,(平角的定义)
∠ADE+∠BCF=180°,(已知)
∴∠ADF=∠BCF,(同角的补角相等 )
∴AD∥BC
(2)解:结论:AB与EF的位置关系是:AB∥EF,
∵BE平分∠ABC,(已知)
∴∠ABE=![]() ∠ABC.(角平分线的定义)
∠ABC.(角平分线的定义)
又∵∠ABC=2∠E,(已知),
即∠E=![]() ∠ABC,
∠ABC,
∴∠E=∠ABE.(等量代换)
∴AB∥EF.(内错角相等,两直线平行 )
故答案为BCF,同角的补角相等,AB∥EF,ABE,等量代换,AB,EF,内错角相等,两直线平行.
(3)证明:①∵AB∥EF,
∴∠BAF=∠F,
∵∠BAD=2∠BAF,
∴∠BAD=2∠F.
②∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵∠OAB=![]() DAB,∠OBA=
DAB,∠OBA=![]() ∠CBA,
∠CBA,
∴∠OAB+∠OBA=90°,
∴∠EOF=∠AOB=90°,
∴∠E+∠F=90°.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 不与点
不与点![]() ,点
,点![]() 重合),在
重合),在![]() 上取一点
上取一点![]() ,且∠CDE=50°.
,且∠CDE=50°.

(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 是等腰三角形时,
是等腰三角形时,![]() 的度数为
的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.
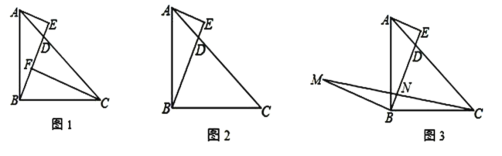
(1) 如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;
(2) 如图 2,若 BC=CD,求证:BD=2AE ;
(3) 如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】空中的气温![]() 与距地面的高度
与距地面的高度![]() 有关,某地面气温为
有关,某地面气温为![]() ,且已知离地面距离每升高
,且已知离地面距离每升高![]() ,气温下降
,气温下降![]() .
.
(1)在这个变化过程中, 是自变量, 是因变量;
(2)写出该地空中气温![]() 与高度
与高度![]() 之间的关系式;
之间的关系式;
(3)求空中气温为![]() 处距地面的高度.
处距地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E、K分别在BC、AB上,CE=BK,点G在BA的延盖
长线上,且DG⊥DE.
(1)如图(1)求证:CK=DG;
(2)如图(2)不添加任何辅助线的条件下,直接写出图中所有的与四边形BEDK面积相等
的三角形。
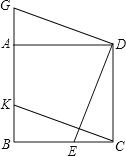
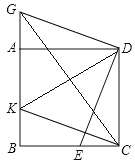
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
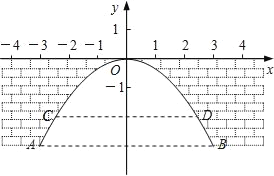
【题目】在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣![]() x2,当水位上涨1m时,水面宽CD为2
x2,当水位上涨1m时,水面宽CD为2![]() m,则桥下的水面宽AB为_____m.
m,则桥下的水面宽AB为_____m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com