练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】负3与2的和是（ ）
    A.5
    B.﹣5
    C.1
    D.﹣1

    【答案】D
    【解析】解：﹣3+2=﹣1．
    故选：D．
    【考点精析】认真审题，首先需要了解有理数的加法法则(有理数加法法则：1、同号两数相加，取相同的符号，并把绝对值相加2、异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值3、一个数与0相加，仍得这个数)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】解答
    （1）如图1，小明和小亮在研究一个数学问题：已知AB∥CD，AB和CD都不经过点P，探索∠P与∠A，∠C的数量关系．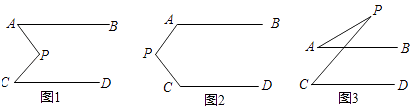

    小明是这样证明的：过点P作PQ∥AB
    ∴∠APQ=∠A（）
    ∵PQ∥AB，AB∥CD．
    ∴PQ∥CD（）
    ∴∠CPQ=∠C
    ∴∠APQ+∠CPQ=∠A+∠C
    即∠APC=∠A+∠C
    小亮是这样证明的：过点作PQ∥AB∥CD．
    ∴∠APQ=∠A，∠CPQ=∠C
    ∴∠APQ+∠CPQ=∠A+∠C
    即∠APC=∠A+∠C
    请在上面证明过程的过程的横线上，填写依据；两人的证明过程中，完全正确的是 ．
    （2）应用：
    在图2中，若∠A=120°，∠C=140°，则∠APC的度数为；
    （3）拓展：
    在图3中，探索∠APC与∠A，∠C的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．
    下面是部分推理过程，请你将其补充完整：
    ∵AD⊥BC于D，EG⊥BC于G （已知）
    ∴∠ADC=∠EGC=90°
    ∴AD∥EG ．
    ∴∠1=∠2 ．
    =∠3（两直线平行，同位角相等）
    又∵∠E=∠1（已知）
    ∴∠2=∠3 ．
    ∴AD平分∠BAC ．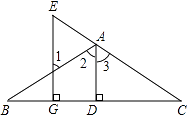

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式能用完全平方公式进行分解因式的是（ ）

    A. x2+1 B. x2+2x﹣1

    C. x2+x+1 D. x2+4x+4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于方程x2+2x﹣4＝0的根的情况，下列结论错误的是（　　）

    A. 有两个不相等的实数根B. 两实数根的和为﹣2

    C. 没有实数根D. 两实数根的积为﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我们认识的多边形中，有很多轴对称图形．有些多边形，边数不同对称轴的条数也不同；有些多边形，边数相同但却有不同数目的对称轴．回答下列问题：
    （1）非等边的等腰三角形有条对称轴，非正方形的长方形有条对称轴，等边三角形有条对称轴；
    （2）观察下列一组凸多边形（实线画出），它们的共同点是只有1条对称轴，其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的，仿照类似的修改方式，请你在图1﹣4和图1﹣5中，分别修改图1﹣2和图1﹣3，得到一个只有1条对称轴的凸五边形，并用实线画出所得的凸五边形；
    （3）小明希望构造出一个恰好有2条对称轴的凸六边形，于是他选择修改长方形，图2中是他没有完成的图形，请用实线帮他补完整个图形；
    （4）请你画一个恰好有3条对称轴的凸六边形，并用虚线标出对称轴．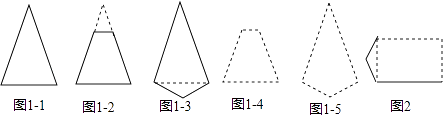

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若﹣2amb4与5an+2b2m+n是同类项，则mn的值是（）
    A.2
    B.0
    C.﹣1
    D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】线段EF是由线段PQ平移得到的，点P（﹣1，4）的对应点为E（4，7），则点Q（﹣3，1）的对应点F的坐标为（）
    A.（﹣8，﹣2）
    B.（﹣2，﹣2）
    C.（2，4）
    D.（﹣6，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB∥CD，∠A=∠D，试说明 AC∥DE 成立的理由．
    （下面是彬彬同学进行的推理，请你将彬彬同学的推理过程补充完整．）
    解：∵AB∥CD （已知）
    ∴∠A=（两直线平行，内错角相等）
    又∵∠A=∠D（）
    ∴∠=∠（等量代换）
    ∴AC∥DE （）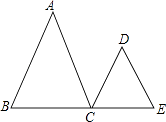

    查看答案和解析>>

    同步练习册答案