
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
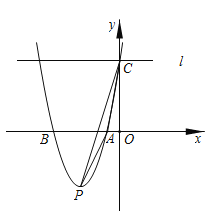
(1)求点![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的3倍?若存在,求出点
的面积的3倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
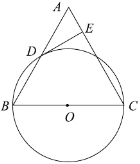
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点.
(2)判断DE与⊙O的位置关系,并证明你的结论.
(3)若⊙O的半径为5,AB=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
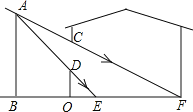
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.9m,窗高CD=1.1m,并测得OE=0.9m,OF=3m,求围墙AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=2x2-4x和一次函数y2=-2x,规定:当x任取一个值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较大值为M;若y1=y2,则M=y1=y2.下列说法错误的是 ( )
A.当x>2时,M=y1B.当x<0时,M随x的增大而减小
C.M的最小值为-2D.若M=-1时,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
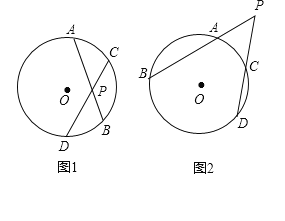
【题目】我们把1°的圆心角所对的弧叫做1°的弧.由此可知:命题“圆周角的度数等于其所对的弧的度数的一半.”是真命题,已知,![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() .
.
(1)如图1,⊙O的两条弦AB、CD相交于圆内一点P,求证:![]() ;
;
(2)如图2,⊙O的两条弦AB、CD延长线相交于圆外一点P.问题(1)中的结论是否成立?如果成立,给予证明;如果不成立,写出一个类似的结论,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() 的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
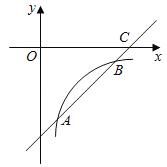
(1)求这两个函数的表达式;
(2)求△AOB的面积;
(3)请直接写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足;当x1<x2<0时(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B、C,且B在C的左侧,△ABC有一个内角为60°.则抛物线的解析式是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从某建筑物9米高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面12米,建立平面直角坐标系,如图.
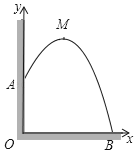
(1)求抛物线的解析式;
(2)求水流落地点B离墙的距离OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销甲、乙两种商品. 现有如下信息:

请根据以上信息,解答下列问题:
(1)甲、乙两种商品的零售单价分别为 元和 元.(直接写出答案)
(2)该商店平均每天卖出甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.为了使每天获取更大的利润,商店决定把甲种商品的零售单价下降x(x>0)元.在不考虑其他因素的条件下,当x定为多少时,才能使商店每天销售甲、乙两种商品获取的利润共1700元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com