
����Ŀ����ͼ������ԭ���������y=��x2��2mx��m��1����x�����һ������ΪA������P����1��m����ֱ��PD��x���ڵ�D�����������ڵ�B��BC��x�ύ�������ڵ�C��
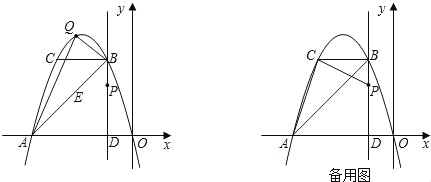
��1����m=2ʱ��
�����߶�BC�ij���ֱ��AB����Ӧ�ĺ�����ϵʽ��
��������Q��ֱ��AB�Ϸ������������˶������Q�ںδ�ʱ����QAB��������
������F���������ϣ���PF=PC����ֱ��д�����������ĵ�F�����ꣻ
��2����m��1ʱ������CA��CP����mΪ��ֵʱ��CA��CP��
���𰸡���1����ֱ��AB����Ӧ�ĺ�����ϵʽΪy=x+4��
����a=-![]() ʱ����QAB��������ʱQ������Ϊ��-
ʱ����QAB��������ʱQ������Ϊ��-![]() ��
��![]() ����
����
�����������ĵ�F����ΪF1����2��0����F2��0��0����F3��0��4����
��2��m=![]() ��
��
��������
�����������1���ٽ�m=2����y=��x2��2mx���ó�y=��x2��4x�����A����4��0����B����1��3������B��C�������������y=��x2��4x�ĶԳ���x=��2�Գƣ��ó�BC=2�����ô���ϵ�������ֱ��AB����Ӧ�ĺ�����ϵʽ��
�ڹ���Q��QE��y�ᣬ��AB�ڵ�E����Q��a����a2��4a������E��a��a+4����QE=����a2��4a������a+4��=��a2��5a��4����S��QAB=![]() QEAD���S��QAB=��
QEAD���S��QAB=��![]() ��a+
��a+![]() ��2+
��2+![]() �����ݶ��κ��������ʼ�����⣻
�����ݶ��κ��������ʼ�����⣻
�۷���������������ۣ�����F��x���ϣ���F��x��0��������PF=PC�г����̣��ⷽ�̵õ�F1����2��0����F2��0��0��������F��y���ϣ���F��0��y��������PF=PC�г����̣��ⷽ�̵õ�F3��0��4����F4��0��0����F2��0��0���غϣ�
��2������C��CH��x���ڵ�H�������PB=m��1��BC=2��m��1����CH=2m��1��AH=1����֤����ACH�ס�PCB���������������ζ�Ӧ�߳ɱ����ó�![]() ����
����![]() ���ⷽ�̿����m��ֵ��
���ⷽ�̿����m��ֵ��
�����������1���ٵ�m=2ʱ��y=��x2��4x��
��y=0���é�x2��4x=0��
���x1=0��x2=��4��
��A����4��0����
��x=��1ʱ��y=3��
��B����1��3����
��������y=��x2��4x�ĶԳ���Ϊֱ��x=��2��
��B��C������ڶԳ���x=��2�Գƣ�
��C����3��3����BC=2��
��ֱ��AB����Ӧ�ĺ�����ϵʽΪy=kx+b��
��A����4��0����B����1��3����ֱ��AB�ϣ�
��![]() �����
�����![]()
��ֱ��AB����Ӧ�ĺ�����ϵʽΪy=x+4��
�ڹ���Q��QE��y�ᣬ��AB�ڵ�E����ͼ1����
���������Q��a����a2��4a������E��a��a+4����
��QE=����a2��4a������a+4��=��a2��5a��4��
��S��QAB=![]() QEAD=
QEAD=![]() ������a2��5a��4����3=��
������a2��5a��4����3=��![]() ��a+
��a+![]() ��2+
��2+![]() ��
��
����a=-![]() ʱ����QAB��������ʱQ������Ϊ��-
ʱ����QAB��������ʱQ������Ϊ��-![]() ��
��![]() ����
����
�۷����������
����F��x���ϣ���F��x��0����
��PF=PC��P����1��2����C����3��3����
����x+1��2+��2��0��2=����3+1��2+��3��2��2��
��������x2+2x=0��
���x1=��2��x2=0��
��F1����2��0����F2��0��0����
����F��y���ϣ���F��0��y����
��PF=PC��P����1��2����C����3��3����
����0+1��2+��y��2��2=����3+1��2+��3��2��2��
��������y2��4y=0��
���y1=4��y2=0��
��F3��0��4����F4��0��0����F2��0��0���غϣ�
�������������������ĵ�F����ΪF1����2��0����F2��0��0����F3��0��4����
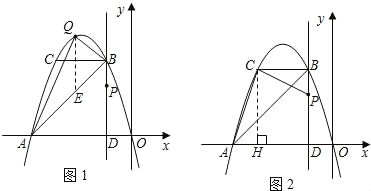
��2������C��CH��x���ڵ�H����ͼ2������P����1��m����B����1��2m��1����
��PB=m��1����������y=��x2��2mx�ĶԳ���Ϊֱ��x=��m������m��1��
��B��C������ڶԳ���x=��m�Գƣ���BC=2��m��1����
��C��1��2m��2m��1����H��1��2m��0������CH=2m��1����A����2m��0������AH=1��
����֪������ACP=��BCH=90�㣬���ACH=��PCB�����ߡ�AHC=��PBC=90�㣬
���ACH�ס�PCB����![]() ����
����![]() ����m=
����m=![]() ��
��


 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����
A. �����콵��ĸ�����80%����ʾ������80%��ʱ�䶼�ڽ���
B. ����һöӲ�����泯�ϵĸ���Ϊ![]() ����ʾÿ��2�ξ���һ�����泯��
����ʾÿ��2�ξ���һ�����泯��
C. ����Ʊ�н��ĸ���Ϊ1%����ʾ��100�Ų�Ʊ�϶����н�
D. ����һö���������ӣ����ϵĵ���Ϊ2�ĸ���Ϊ![]() ����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���
����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������Ϊ������������������ʵЧ�����������˲��־���С��һ��ʱ�������������ķ��������������������������������������ͳ��ͼ��
����ͳ��ͼ����������⣺
��1�����������������������ܶ����Լ����е��к������Ķ�����
��2��������ͳ��ͼ�У���D����������Ӧ��Բ�ĽǵĶ�������������ͳ��ͼ����������
��3�����鷢�֣��ڿɻ������з�ֽ����Լռ ![]() ��ÿ����1�ַ�ֽ������0.85�ֵ�����ֽ������ó���ÿ����������������Ϊ10000�֣���ȫ�����ദ������ôÿ�»��յķ�ֽ���Ƴ�����ֽ���ٶ֣�
��ÿ����1�ַ�ֽ������0.85�ֵ�����ֽ������ó���ÿ����������������Ϊ10000�֣���ȫ�����ദ������ôÿ�»��յķ�ֽ���Ƴ�����ֽ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB=90�㣬OM�ǡ�AOB��ƽ���ߣ���D�DZ�OB��һ���㣬�����ǰ��ֱ�Ƕ���P������OM���ƶ���ʹһֱ�DZ߾�����D����һֱ�����OA���ڵ�C.����֤��PC=PD����ͼ�٣�
��1������һֱ�DZ����OA�ķ����ӳ����ཻ�ڵ�C(��ͼ��)������PC��PD�������������ȣ�������֤����������ȣ���˵�����ɣ�
��2����֪OD=4�����ǰ����ƶ������У���һֱ�DZ���ֱ��OA��ֱ��OB�ֱ��ڵ�C,E,����P,D,EΪ�������������OCD���ƣ������߶�OP�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ij������Ʒר��������7�������9�������������Ϊ355Ԫ������10�������20�������������Ϊ650Ԫ��
��1����ÿ�������ÿ���������������
��2����֪ÿ������Ľ���Ϊ200Ԫ��ÿ������Ľ���Ϊ160Ԫ������ר����ƻ��ò�����17400Ԫ�������������100������Ҫ��������������������������һ�룬����Ϊר������Ʒ���Ҫ��Ľ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ξ�����Ʊ�۸�涨���£�
ijУ���꼶��֯�ס��������92��ȥ�þ������棬���мװ����������Ұ������Ҽװ���������90�ˣ�����������������Ʊ��һ��Ӧ��7760Ԫ��
��1������ס�����������������������Ʊ����ô�ȸ��Թ�����Ʊ���Խ�ʡ����Ǯ��
��2���ס�����������ж���ѧ����
��3������װ���10��ѧ����ѧУ�������ܲμ�������Σ�������Ϊ��������Ƴ�������Ʊ�ķ�������ָ����ʡǮ�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ ![]() �У�����
������ ![]() ��
�� ![]() ��
�� ![]() �ڵ�
�ڵ� ![]() ��
�� ![]() ��
�� ![]() �ڵ�
�ڵ� ![]() ��
�� ![]() ��
��
��֤���ı��� ![]() �����Σ�
������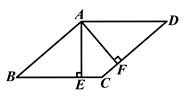
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����ǿѧ�����ʣ�ȫ��ʵʩ��ѧ�������̡�Ӫ�����̣�ijƷ��ţ�̹�Ӧ���ṩ��ԭζ����ݮζ������ζ�����ζ������ζ���ֿ�ζ��ţ���ṩѧ�����ã������ѧΪ���˽�ѧ���Բ�ͬ��ζţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨ÿ�и��ֿ�ζţ�̵������ͬ������������ͼ���Ų�����������ͳ��ͼ��
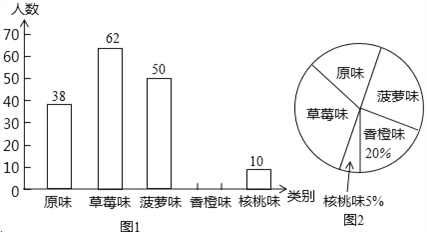
��1�����α������ѧ������ ������
��2����ȫ���������ͳ��ͼ1���������ϲ�á�����ζ��ţ�̵�ѧ������������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3����У����1200��ѧ�������˸�Ʒ�Ƶ�ţ�̣�ţ�̹�Ӧ��ÿ��ֻΪÿ������ţ�̵�ѧ������һ��ţ�̣�Ҫʹѧ��ÿ�춼�ȵ��Լ�ϲ�õĿ�ζ��ţ�̣�ţ�̹�Ӧ��ÿ��������У��ţ���У���ݮζҪ��ԭζ���Ͷ��ٺУ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com