
分析 (1)由△=36-4(3m-2)≥0,得到m≤$\frac{11}{3}$,设方程的两根为x1,x2,根据根与系数的关系得到x1+x2=6,x1•x2=3m-2,由于方程有两个正根,于是得到x1•x2=3m-2>0,即可得到结果;
(2)由于方程的两个根都大于1,于是得到(x1-1)(x2-1)=x1•x2-(x1+x2)+1>0,解不等式3m-2-6+1>0,即可得到m的取值范围:
(3)一个根大于1,另一个根小于1,即方程两根与1的差的乘积是负数,根据一元二次方程根与系数的关系表示出两根的和与两根的积,根据(x1-1)(x2-1)=x1x2-(x1+x2)+1,即可得到关于m的方程,即可求得m的值,
(4)由方程x2-6x+3m-2=0两个根分别位于区间(0,1)和(4,5)上,得到对应的方程的两个根分别位于区间(0,1)和(4,5)各有一个零点,于是得到$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(4)•f(5)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{(3m-2)•(3m-7)<0}\\{(3m-10)(3m-7)<0}\end{array}\right.$,解得m的取值范围即可.
解答 解:∵△=36-4(3m-2)≥0,
∴m≤$\frac{11}{3}$,
设方程的两根为x1,x2,
∴x1+x2=6,x1•x2=3m-2,
(1)∵方程有两个正根,
∴x1•x2=3m-2>0,
∴m>$\frac{2}{3}$,
∴若方程有两个正根,m的取值范围:$\frac{2}{3}$<m≤$\frac{11}{3}$,
(2)∵若方程的两个根都大于1,
∴(x1-1)(x2-1)=x1•x2-(x1+x2)+1>0,
∴3m-2-6+1>0,
∴m>$\frac{7}{3}$,
∴若方程的两个根都大于1,m的取值范围:$\frac{7}{3}$<m≤$\frac{11}{3}$;
(3)设两根为x1>1,x2<1.
那么x1-1>0,x2-1<0.
∴(x1-1)(x2-1)<0.
x1x2-(x1+x2)+1<0.
∴3m-2-6+1<0,
∴m$<\frac{7}{3}$;
(4)设f(x)=x2-6x+3m-2=0,则f(x)=0的两个根分别属于(0,1)和(4,5),
∴$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(4)•f(5)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{(3m-2)•(3m-7)<0}\\{(3m-10)(3m-7)<0}\end{array}\right.$,
解得:$\frac{2}{3}$<m<$\frac{7}{3}$.
点评 本题考查了根的判别式,根与系数的关系,根据题意正确的列出不等式是解题的关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:选择题
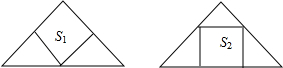 如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com