
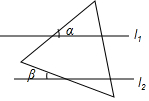
 如图,已知直线L1∥L2,将等边三角形如图放置,若∠ɑ=40°,则∠β等于20°.
如图,已知直线L1∥L2,将等边三角形如图放置,若∠ɑ=40°,则∠β等于20°. 分析 过点A作AD∥l1,如图,根据平行线的性质可得∠BAD=∠β.根据平行线的传递性可得AD∥l2,从而得到∠DAC=∠α=40°.再根据等边△ABC可得到∠BAC=60°,就可求出∠DAC,从而解决问题.
解答 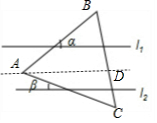 解:过点A作AD∥l1,如图,
解:过点A作AD∥l1,如图,
则∠BAD=∠β.
∵l1∥l2,
∴AD∥l2,
∵∠DAC=∠α=40°.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠β=∠BAD=∠BAC-∠DAC=60°-40°=20°.
故答案为20°.
点评 本题主要考查了平行线的性质、平行线的传递性、等边三角形的性质等知识,当然也可延长BA与l2交于点E,运用平行线的性质及三角形外角的性质解决问题.


科目:初中数学 来源: 题型:填空题
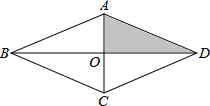 如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是$\frac{1}{4}$.
如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
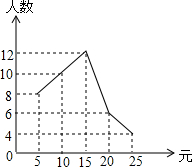 某班全体学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中捐款额的中位数是15元.
某班全体学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中捐款额的中位数是15元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
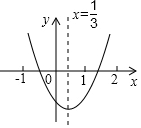 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①abc>0;②a-b+c>0;③4a+2b+c<0;④2a-3b=0;⑤c-4b>0,其中正确的有( )
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①abc>0;②a-b+c>0;③4a+2b+c<0;④2a-3b=0;⑤c-4b>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
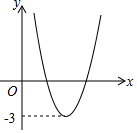 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k 的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k 的取值范围是( )| A. | k<-3 | B. | k>-3 | C. | k<3 | D. | k>3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com