
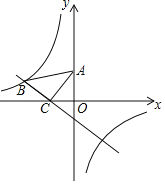
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ���C����Ϊ����1��0������A����Ϊ��0��2����һ�κ���y��kx+b��ͼ����B��C������������y��![]() ��ͼ����B��
��ͼ����B��
��1����һ�κ����ͷ����������Ĺ�ϵʽ��
��2��ֱ��д����x��0ʱ��kx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
��3����x������һ��M��ʹ��AM+BM��ֵ��С��ֱ��д����M�������AM+BM����Сֵ��
���𰸡���1��y����![]() x��
x��![]() ��y����
��y����![]() ����2����3��x��0����3����M������Ϊ����2��0����AM+BM����СֵΪ3
����2����3��x��0����3����M������Ϊ����2��0����AM+BM����СֵΪ3![]() ��
��
��������
��1������B��BF��x���ڵ�F������AOC�ա�CFB��õ�B�����꣬���ô���ϵ���������һ�κ����ͷ����������Ĺ�ϵʽ��
��2����x��0ʱ�����һ�κ���ֵy��kx+bС�ڷ���������y��![]() ��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��x��ȡֵ��Χ�����ͼ�μ���ֱ��д���𰸣�
��3��������ԳƵ����ʣ��ҵ���A����x�ĶԳƵ�A��������BA������BA����x��Ľ��㼴Ϊ��M��λ�ã����ֱ��BA���Ľ���ʽ���ɵó���M�����꣬����B��A������������AM+BM����Сֵ��
�⣺��1������B��BF��x���ڵ�F��
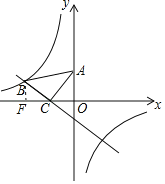
�ߵ�C����Ϊ(��1,0)����A����Ϊ��0,2����
��OA��2��OC��1��
�ߡ�BCA��90����
���BCF+��ACO��90����
�֡ߡ�CAO+��ACO��90����
���BCF����CAO��
����AOC����CFB��
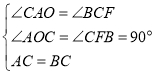
���AOC�ա�CFB��AAS����
��FC��OA��2��BF��OC��1��
���B����������3��1����
����B��������뷴������������ʽ�ɵã� ![]() ��
��
��ã�k����3��
�ʿɵ÷�������������ʽΪy����![]() ��
��
����B��C���������һ�κ�������ʽ�ɵã�![]() ��
��
��ã�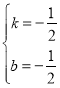 ��
��
�ʿɵ�һ�κ�������ʽΪ![]() ��
��
��2����ϵ�B�����꼰ͼ�ɵõ�x��0ʱ��![]() ��0�Ľ⼯Ϊ����3��x��0��
��0�Ľ⼯Ϊ����3��x��0��
��3������A����x��ĶԳƵ�A�������� B A����x�� �Ľ��㼴Ϊ��M��
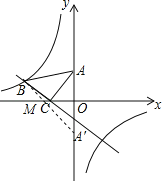
��A��0��2��������A����x��ĶԳƵ�A����
��A����0����2����
��ֱ��BA���Ľ���ʽΪy��ax+b������A������B���������ɵã�![]()
��ã�![]() ��
��
��ֱ��BA���Ľ���ʽΪy����x��2��
��y��0���ɵé�x��2��0��
��ã�x����2��
�ʵ�M ������Ϊ����2��0����
AM+BM��BM+MA����BA����![]() ��
��
���Ͽɵã���M������Ϊ����2��0����AM+BM����СֵΪ![]() ��
��


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
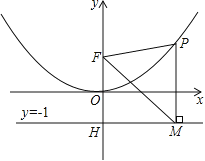
����Ŀ�����κ���ͼ��Ķ�����ԭ��O��������A��1��![]() ������F��0��1����y���ϣ�ֱ��y=��1��y�ύ�ڵ�H��
������F��0��1����y���ϣ�ֱ��y=��1��y�ύ�ڵ�H��
��1������κ����Ľ���ʽ��
��2����P�ǣ�1����ͼ���ϵĵ㣬����P��x��Ĵ�����ֱ��y=��1���ڵ�M����֤��FMƽ����OFP��
��3������FPM�ǵȱ�������ʱ����P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
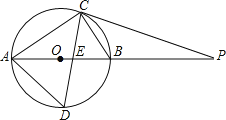
����Ŀ����ͼ��O��ֱ��AB��10cm����BC��6cm����ACB��ƽ���߽���O��D����AB��E��P��AB�ӳ�����һ�㣬��PC��PE��
(l)��֤��PC�ǡ�O�����ߣ�
(2)��AC��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ xOy�У����������� y ![]() x 0 ��ͼ���� A2,3 ��ֱ��y ax �� y
x 0 ��ͼ���� A2,3 ��ֱ��y ax �� y ![]() �뷴�������� y
�뷴�������� y ![]() x 0 �ֱ��ڵ� B��C���㣮
x 0 �ֱ��ڵ� B��C���㣮
��1��ֱ��д�� k ��ֵ ��
��2�����߶� OB��OC�ͺ��� y ![]() x 0 �� B��C ֮��IJ���Χ�ɵ�����(�����߽�)Ϊ W��
x 0 �� B��C ֮��IJ���Χ�ɵ�����(�����߽�)Ϊ W��
�� �� A���� B���غ�ʱ��ֱ��д������ W �ڵ�������� ��
�� ������ W��ǡ�� 8�����㣬��Ϻ���ͼ��ֱ��д�� a��ȡֵ��Χ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
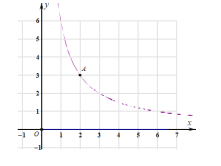
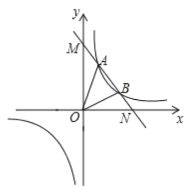
����Ŀ����ͼ��һ�κ���![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�A(
��ͼ���ڵ�A(![]() )��
)��![]() ���㣬��������ֱ���M��N���㣮
���㣬��������ֱ���M��N���㣮
��1����һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д��![]() ��
��![]() ��ȡֵ��Χ��____________��
��ȡֵ��Χ��____________��
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������CGFE�Ķ���C��D��E��ͬһ��ֱ���ϣ�����B��C��G��ͬһ��ֱ���ϣ�O��EG���е㣬��EGC��ƽ����GH����D����BE�ڵ�H������FH��EG�ڵ�M������OH�������ĸ����ۣ���GH��BE������EHM�ס�GHF����![]() ��1����
��1����![]() ��2��
��2��![]() ��������ȷ�Ľ����ǣ�������
��������ȷ�Ľ����ǣ�������
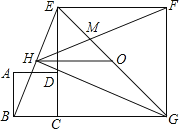
A. �٢ڢ�B. �٢ڢ�C. �٢ۢ�D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı��ε�һ���Խ��߽�����ı��ηֳ����������Σ��������������������(��ȫ��)����ô���ǽ������Խ��߽�������ı��ε����ƶԽ��ߣ�
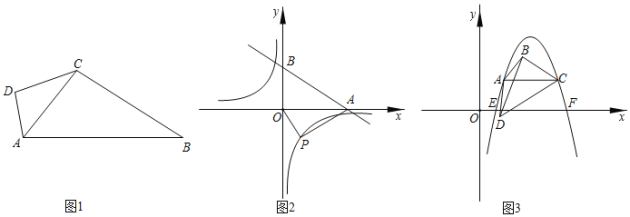
(1)��ͼ1���ı���ABCD�У���DAB��100������DCB��130�����Խ���ACƽ�֡�DAB����֤��AC���ı���ABCD�����ƶԽ��ߣ�
(2)��ͼ2��ֱ��![]() �ֱ���x��y���ཻ��A��B���㣬PΪ����������y��
�ֱ���x��y���ཻ��A��B���㣬PΪ����������y��![]() (k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
(k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
(3)��ͼ3��AC���ı���ABCD�����ƶԽ��ߣ���C������Ϊ(3��1)��AC��x�ᣬ��BCA����DCA��30��������BD����BCD�����Ϊ![]() ����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㵺�Թ����������й�����ʥ������Ϊ������Ȩ���Һ��ബ��ӷ����ڵ��㵺�����������άȨ�����ͼ��һ�Һ��ബ��30����/Сʱ���ٶ������������У����ബ��A��ʱ����õ��㵺C�ڸô��ı�ƫ��30�������ϣ����а�Сʱ�ô������B�������ִ�ʱ���㵺C��ô�������̣�
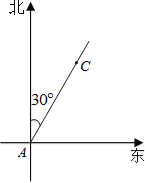
��1������ͼ�������ô��ڵ�B����λ�ã�
��2������㵺C��B�����루����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
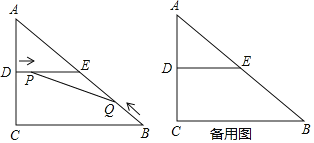
����Ŀ����ͼ���ڡ�ABC�У���C��90����AC��12cm��BC��16cm��D��E�ֱ���AC��AB���е㣬����DE����P�ӵ�D��������DE���������˶����ٶ�Ϊ2cm/s��ͬʱ����Q�ӵ�B��������BA���������˶����ٶ�Ϊ4cm/s������Pֹͣ�˶�ʱ����QҲֹͣ�˶�������PQ�����˶�ʱ��Ϊt��0��t��4��s������������⣺
��1����tΪ��ֵʱ���Ե�E��P��QΪ��������������ADE���ƣ�
��2����tΪ��ֵʱ����EPQΪ���������Σ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com