
【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 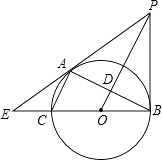
(1)求证:PA是⊙O的切线;
(2)若sinE= ![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
【答案】
(1)证明:连接OA,如图,
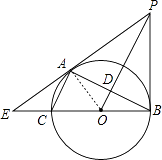
∵AC∥OP,
∴∠ACO=∠POB,∠CAO=∠POA,
又∵OA=OC,
∴∠ACO=∠CAO,
∴∠POA=∠POB,
在△PAO和△PBO中,
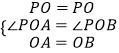 ,
,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO,
又∵PB⊥BC,
∴∠PBO=90°,
∴∠PAO=90°,
∴OA⊥PE,
∴PA是⊙O的切线
(2)解:∵△PAO≌△PBO,
∴PB=PA=6,
在Rt△PBE中,∵sinE= ![]() =
= ![]()
∴ ![]() =
= ![]() ,解得PE=10,
,解得PE=10,
∴AE=PE﹣PA=4,
在Rt△AOE中,sinE= ![]() =
= ![]() ,
,
设OA=3t,则OE=5t,
∴AE= ![]() =4t,
=4t,
∴4t=4,解得t=1,
∴OA=3,
在Rt△PBO中,∵OB=3,PB=6,
∴OP= ![]() =3
=3 ![]() ,
,
∵AC∥OP,
∴△EAC∽△EPO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC= ![]() .
.
【解析】(1)先利用平行线的性质得到∠ACO=∠POB,∠CAO=∠POA,加上∠ACO=∠CAO,则∠POA=∠POB,于是可根据“SAS”判断△PAO≌△PBO,则∠PAO=∠PBO=90°,然后根据切线的判定定理即可得到PA是⊙O的切线;(2)先由△PAO≌△PBO得PB=PA=6,在Rt△PBE中,利用正弦的定义可计算PE=10,则AE=PE﹣PA=4,再在Rt△AOE中,由sinE= ![]() =
= ![]() ,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3
,可设OA=3t,则OE=5t,由勾股定理得到AE=4t,则4t=4,解得t=1,所以OA=3;接着在Rt△PBO中利用勾股定理计算出OP=3 ![]() ,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
,然后证明△EAC∽△EPO,再利用相似比可计算出AC.
【考点精析】根据题目的已知条件,利用切线的判定定理的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.
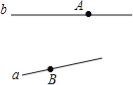
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明(在下面的括号内填上相应的结论或推理的依据):如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,
求证:AD是∠BAC的平分线.
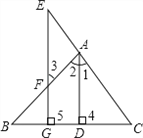
证明:∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°( )
∴AD∥EG( )
∴∠1=∠E( ) ∠2=∠3( )
∵∠E=∠3(已知)
∴( )=( )
∴AD是∠BAC的平分线( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,即可求出x的值.参考小萍的思路,探究并解答新问题:如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭绍台高铁项目是国内首批八个社会资本投资铁路示范项目之一,也是中国首个民营控股高速铁路项目.该项目可用批复总投资预计448.9亿元,资本金占总投资的30%,其中民营联合体占股51%,其中448.9亿元用科学记数法表示为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 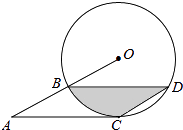
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com