
【题目】如图,在ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°

(1)求∠BAC的度数;
(2)若BD=2,求CD的长.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子![]() 米跑项目,该校预先对这两名选手测试了
米跑项目,该校预先对这两名选手测试了![]() 次,测试成绩如下表
次,测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩(秒) |
|
|
|
|
|
|
|
|
乙的成绩(秒) |
|
|
|
|
|
|
|
|
![]() 为了衡量这两名选手
为了衡量这两名选手![]() 米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
![]() 你认为选派谁比较合适?为什么?
你认为选派谁比较合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011?菏泽)如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
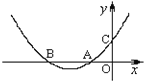
A. a+b=﹣1 B. a﹣b=﹣1
C. b<2a D. ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
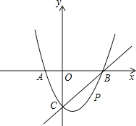
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左则,
点在原点的左则,![]() 点的坐标为
点的坐标为![]() ,与
,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
![]() 求这个二次函数的表达式;
求这个二次函数的表达式;
![]() 求出四边形
求出四边形![]() 的面积最大时的
的面积最大时的![]() 点坐标和四边形
点坐标和四边形![]() 的最大面积;
的最大面积;
![]() 连结
连结![]() 、
、![]() ,在同一平面内把
,在同一平面内把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() ,是否存在点
,是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 在直线
在直线![]() 找一点
找一点![]() ,使得
,使得![]() 为等腰三角形,请直接写出
为等腰三角形,请直接写出![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
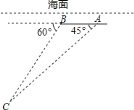
【题目】如图,埃航![]() 客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下
客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下![]() 米的
米的![]() 点处测得俯角为
点处测得俯角为![]() 的前下方海底有黑匣子信号发出,继续沿原方向直线航行
的前下方海底有黑匣子信号发出,继续沿原方向直线航行![]() 米后到达
米后到达![]() 点,在
点,在![]() 处测得俯角为
处测得俯角为![]() 的前下方海底有黑匣子信号发出,求海底黑匣子
的前下方海底有黑匣子信号发出,求海底黑匣子![]() 点距离海面的深度(结果保留根号).
点距离海面的深度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
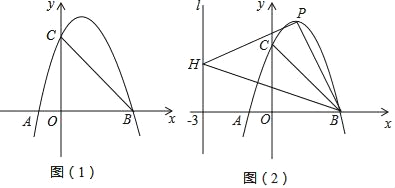
【题目】如图(1),已知抛物线E:y=ax2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),对称轴为直线x=1.
(1)填空:a= ,b= ,c= ;
(2)将抛物线E向下平移d个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求d的取值范围;
(3)如图(2),设点P是抛物线E上任意一点,点H在直线x=﹣3上,△PBH能否成为以点P为直角顶点的等腰直角三角形?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com