
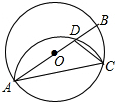
 如图,AB为⊙O的直径,点C为圆上一点,∠BAC=25°,若将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD,则∠DCA的度数为( )
如图,AB为⊙O的直径,点C为圆上一点,∠BAC=25°,若将劣弧$\widehat{AC}$沿弦AC翻折交AB于点D,连结CD,则∠DCA的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
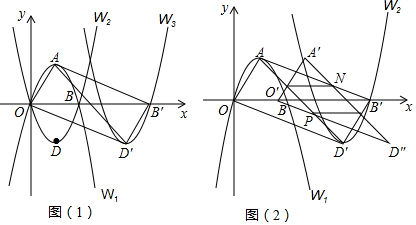
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
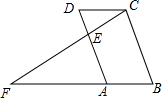 如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在平行四边形ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | ∠AEF=∠DEC | B. | BC:DE=CF:CE | C. | FA:AB=FE:EC | D. | FA:CD=AD:DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
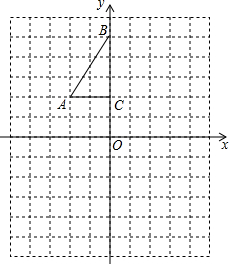 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com