
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图,若a=4,b=6,则该直角三角形的周长为( )
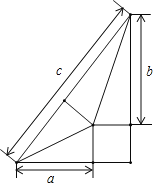
A.18B.20C.24D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).

(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为_____m2.
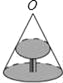
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A.点![]() 在它的图象上
在它的图象上
B.它的图象在第一、三象限
C.当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
D.如果点![]() 在它的图象上,则点
在它的图象上,则点![]() 不在它的图象上
不在它的图象上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
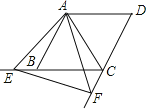
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:当a>0且x>0时,因为 ≥0,所以
≥0,所以![]() ,从而
,从而![]() ≥
≥![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数![]() =
=![]() (
(![]() >0,x>0),由上述结论可知,当x=
>0,x>0),由上述结论可知,当x=![]() 时,该函数有最小值为
时,该函数有最小值为![]() .
.
应用举例:已知函数![]() =x(x>0)与函数
=x(x>0)与函数![]() =
=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,
=2时,![]() =
=![]() 有最小值为
有最小值为![]() =4.
=4.
解决问题:
(1)已知函数![]() =
=![]() (x>-3)与函数
(x>-3)与函数![]() =
=![]() (x>-3),当x为何值时,
(x>-3),当x为何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,连接BC.
(1)求直线BC的解析式;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ∥y轴交BC于Q,当线段PQ的长度最大时,在x轴上找一点M,使PM+CM的值最小,求PM+CM的最小值;
(3)抛物线的顶点为点E,连接AE,在抛物线上是否存在一点N,使得直线AN与直线AE的夹角为45度,若存在请直接写出满足条件的点N的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.

(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com