
【题目】已知不等臂跷跷板AB长为3米,跷跷板AB的支撑点O到地面上的点H的距高OH=0.6米。当跷跷板AB的一个端点A碰到地面时,AB与地面上的直线AH的夹角∠OAH的度数为30°.
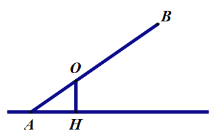
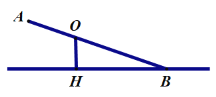
(1)当AB的另一个端点B碰到地面时(如右图),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?
(2)当AB的另一个端点B碰到地面时(如右图),点A到直线BH的距离是多少米?
科目:初中数学 来源: 题型:
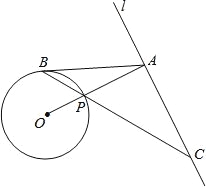
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=![]() ,OA=3,求⊙O的半径和线段PB的长.
,OA=3,求⊙O的半径和线段PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为【 】

A.1 B.![]() C. 2 D.
C. 2 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣3=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为非负整数,且该方程的根都是无理数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有两点![]() ,若二次函数
,若二次函数![]() 的图像与线段AB只有一个交点,则( )
的图像与线段AB只有一个交点,则( )
A.![]() 的值可以是
的值可以是![]() B.
B.![]() 的值可以是
的值可以是![]()
C.![]() 的值不可能是-1.2D.
的值不可能是-1.2D.![]() 的值不可能是-1
的值不可能是-1
查看答案和解析>>
科目:初中数学 来源: 题型:
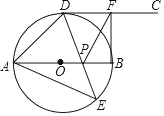
【题目】如图,AB为⊙O的直径,点D、E位于AB两侧的半圆上,射线DC切⊙O于点D,已知点E是半圆弧AB上的动点,点F是射线DC上的动点,连接DE、AE,DE与AB交于点P,再连接FP、FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①当∠DAE= 时,四边形ADFP是菱形;
②当∠DAE= 时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
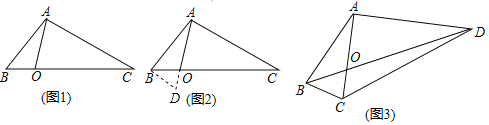
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com