
分析 (1)先算括号内的乘法,再算乘方;先乘方,再算乘法;
②根据有理数乘方的定义求出即可;
③根据同底数幂的乘法计算,再根据积的乘方计算,即可得出答案.
解答 解:(1)(2×$\frac{1}{2}$)100=1,2100×($\frac{1}{2}$)100=1;
②(a•b)n=anbn,(abc)n=anbncn,
③原式=(-0.125)2015×22015×42015×[(-0.125)×(-0.125)×2]
=(-0.125×2×4)2015×$\frac{1}{32}$
=(-1)2015×$\frac{1}{32}$
=-1×$\frac{1}{32}$
=-$\frac{1}{32}$.
故答案为:1,1;anbn,anbncn.
点评 本题主要考查了同底数幂的乘法和积的乘方,掌握运算法则是解答此题的关键.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国古代数学中有一道数学题:如图,有一棵枯树直立在地上,树高20尺,粗3尺,有一根藤条从树根处缠绕而上,缠绕5周到达树顶,则这条树藤有25尺.
我国古代数学中有一道数学题:如图,有一棵枯树直立在地上,树高20尺,粗3尺,有一根藤条从树根处缠绕而上,缠绕5周到达树顶,则这条树藤有25尺.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
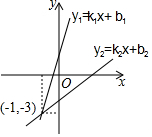 如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.
如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
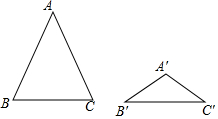 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠A与∠A′互补,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠A与∠A′互补,则△ABC与△A′B′C′的面积比为( )| A. | $\sqrt{5}$:$\sqrt{3}$ | B. | 5:3 | C. | 25:9 | D. | 5$\sqrt{5}$:3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5×1011千克 | B. | 50×109千克 | C. | 5×109千克 | D. | 5×1010千克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com