
【题目】如图,点D、E、F分别在正三角形ABC的三边上,且△DEF也是正三角形,若△ABC的边长为a,△DEF的边长为b.则△AEF的内切圆半径为 . 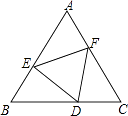
【答案】![]() (a﹣b)
(a﹣b)
【解析】解:如图,由于△ABC,△DEF都为正三角形, ∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
在△AEF和△CFD中,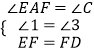 ,
,
∴△AEF≌△CFD(AAS);
同理可证:△AEF≌△CFD≌△BDE;
∴BE=AF,即AE+AF=AE+BE=a.
设M是△AEF的内心,MH⊥AE于H,
则AH= ![]() (AE+AF﹣EF)=
(AE+AF﹣EF)= ![]() (a﹣b);
(a﹣b);
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°= ![]() (a﹣b)
(a﹣b) ![]() =
= ![]() (a﹣b).
(a﹣b).
所以答案是: ![]() (a﹣b).
(a﹣b).
【考点精析】本题主要考查了等边三角形的性质和三角形的内切圆与内心的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即![]() =3+5;
=3+5;![]() =7+9+11;
=7+9+11;![]() =13+15+17+19;…;若
=13+15+17+19;…;若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:![]()
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
A. 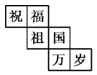 B.
B. 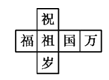 C.
C. 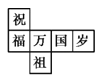 D.
D. 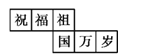
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按规律排列的一列数:
第1个式子:1-![]() ;
;
第2个式子:2-![]() ×
×![]() ×
×![]() ;
;
第3个式子:3-![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() .
.
(1)分别计算这三个式子的结果(直接写答案);
(2)写出第2018个式子的形式(中间部分用省略号,两端部分必须写详细),然后计算出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 . 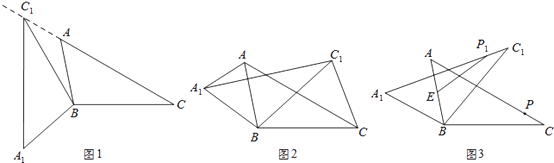
(1)如图1,当点C1在线段CA的延长线时,求∠CC1A1的度数;
(2)已知AB=6,BC=8,
①如图2,连接AA1 , CC1 , 若△CBC1的面积为16,求△ABA1的面积;
②如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应是点P1 , 直接写出线段EP1长度的最大值.
(3)线段EP1长度的最大值为11,理由如下:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
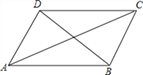
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com