
 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
分析 (1)用总人数20减去其它各岗位人数得到助理人数,进而可将各岗位人数统计图补充完整;
(2)根据员工基本工资的平均数为2200元即可求解;
(3)求公司所有员工基本工资的中位数,可先将表中的数据进行从小到大的排列,由于员工的人数为20人,因此排列后的数据中第10个与第11个数的平均数就是所求的中位数.众数是出现次数最多的数,看哪个数出现的频率最高,那个数就是这组数据的众数;要表示该公司的月工资的一般化水平应该是中位数和众数更合适.
解答 解:(1)助理的人数是:20-1-2-2-8-2=5(人),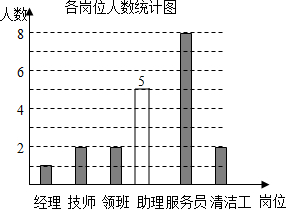 ;
;
(2)解:(2200×20-10000-4000×2-2400×2-1600×5-1000×2)÷8
=1400(元);
(3)中位数是1500,众数是1400.
答:中位数能代表该公司员工的基本工资水平.
故答案为:1500,1400.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:(其中∠A=60°,∠D=30°,∠B=∠E=45°,)
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:(其中∠A=60°,∠D=30°,∠B=∠E=45°,)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=CD,AD=BC,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.
如图,在四边形ABCD中,AB=CD,AD=BC,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com