
分析 此题经观察可知a-b=-1,b-c=-1,a-c=-2,再把多项式转化为完全平方形式,再代入值求解即可.
解答 解:由题意可知:a-b=-1,b-c=-1,a-c=-2,
则a2+b2+c2-ab-bc-ca=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2bc-2ca)
=$\frac{1}{2}$[(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)]
=$\frac{1}{2}$[(a-b)2+(b-c)2+(a-c)2]
=$\frac{1}{2}$[(-1)2+(-1)2+(-2)2]
=3.
点评 本题考查了因式分解的应用,属于基础题,关键在于灵活思维,对多项式扩大2倍是利用完全平方公式的关键.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
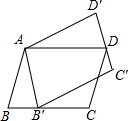 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )| A. | 105° | B. | 150° | C. | 75° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
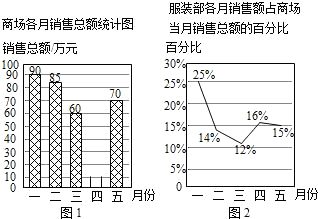
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com