
如图,二次函数y=x2+bx-3b+3的图象与x轴交于A、B两点(点A在点B的左边),交y轴于点C,且经过点(b-2,2b2-5b-1).
(1)求这条抛物线的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求点M的坐标;
(3)连接AM、DM,将∠AMD绕点M顺时针旋转,两边MA、MD与x轴、y轴分别交于点E、F,若△DMF为等腰三角形,求点E的坐标.
 |
解析:(1)把点(b-2,2b2-5b-1)代入解析式,得
2b2-5b-1=(b-2)2+b(b-2)-3b+3,
解得b=2.
∴抛物线的解析式为y=x2+2x-3.
(2)由x2+2x-3=0,得x=-3或x=1.
∴A(-3,0)、B(1,0)、C(0,-3).
抛物线的对 称轴是直线x=-1,圆心M在直线x=-1上.
称轴是直线x=-1,圆心M在直线x=-1上.
∴设M(-1,n),作MG⊥x轴于G,MH⊥y轴于H,
连接MC、MB.
∴MH=1,BG=2.
∵MB=MC,∴BG2+MG2=MH2+CH2,
即4+n2=1+(3+n)2,解得n=-1,∴点M(-1,-1)
(3)如图,由M(-1,-1),得MG=MH.
∵MA=MD,∴Rt△AMG≌RtDMH,∴∠1=∠2.
由旋转可知∠3=∠4. ∴△AME≌△DMF.
若△DMF为等腰三角形,则△AME为等腰三角形.
设E(x,0),△AME为等腰三角形,分三种情况:
①AE=AM= ,则x=
,则x= -3,∴E(
-3,∴E( -3,0);
-3,0);
②∵M在AB的垂直平分线上,
∴MA=ME=MB,∴E(1,0)
③点E在AM的垂直平分线上,则AE=ME.
AE=x+3,ME2=MG2+EG2=1+(-1-x)2,∴(x+3)2=1+(-1-x)2,解得x= ,∴E(
,∴E( ,0).∴所求点E的坐标为(
,0).∴所求点E的坐标为( -3,0),(1,0),(
-3,0),(1,0),( ,0)
,0)
 |


科目:初中数学 来源: 题型:
在毕业联欢晚会上,有A、B、C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点 B.三条角平分线的交点
C.三边上高的交点 D.三边垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
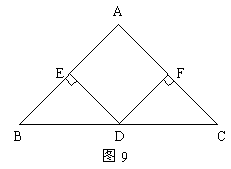
如图9,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F。
求证:(1)△BDE≌△CDF;
(2)∠A=90°时,四边形AEDF是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
目前我市“校园手机”现象越来越受到社会关注,针对这种现象,我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法,统计整理并制作了如下的统计图:
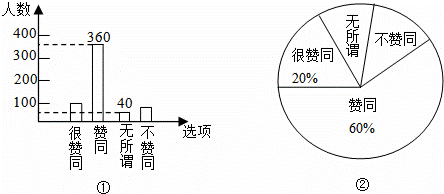
(1)这次调查的家长总数为 .家长表示“不赞同”的人数为 ;
(2)从这次接受调查的家长中随机抽查一个,恰好是“赞同”的家长的概率是 ;
(3)求图②中表示家长“无所谓”的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、直角梯形、矩形、圆,在看不见图形的情况下随机摸出1张,这张卡片上的图形既是中心对称图形又是轴对称图形的概率是( )
A. B.
B.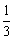 C.
C. D.
D.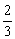
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com