
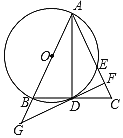
【题目】如图,△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=![]() ,CF=2,求DF和BG的长.
,CF=2,求DF和BG的长.
【答案】(1)见解析;(2)DF=4,BG=![]()
【解析】
(1)连接OD,根据圆周角定理得到AD⊥BC,结合等腰三角形的性质知BD=CD,再根据OA=OB知OD∥AC,从而由DF⊥AC可得OD⊥DF,即可得证;
(2)连接BE.BE∥DF,可得DF是△BEC的中位线,设AE=x,则AC=AB=x+4,根据勾股定理列方程可得x的值,证明△GOD∽△GAF,列比例式可得BG的长.
(1)∵AB是⊙O的直径,
∴∠ADB=90°,
连接OD,
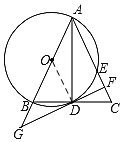
∵∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
又∵OA=OB,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是圆O的切线;
(2)连接BE.
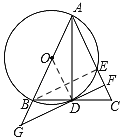
∵CD=BD=2![]() ,
,
∵CF=2,
∴![]() ,
,
∵AB是直径,
∴∠AEB=∠CEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴DF∥BE,
∴EF=FC=2,
∴BE=2DF=8,
设AE=x,则AC=AB=x+4
由勾股定理得:AB2=AE2+BE2,
(x+4)2=82+x2,
x=6,
∴AE=6,AB=4+6=10,
∵OD∥AF,
∴△GOD∽△GAF,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() .
.


科目:初中数学 来源: 题型:
【题目】我县寿源壹号楼盘准备以每平方米![]() 元均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望,房地产开发商为了加快资金周转,对价格进行两次下调后,决定以每平方米
元均价对外销售,由于国务院有关房地产的新政策出台,购房者持币观望,房地产开发商为了加快资金周转,对价格进行两次下调后,决定以每平方米![]() 元的均价开盘销售.
元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘均价购买一套![]() 平方米的住房,开发商给予以下两种优惠方案供选择:
平方米的住房,开发商给予以下两种优惠方案供选择:
①打![]() 折销售;
折销售;
②不打折,一次性送装修费每平方米![]() 元.
元.
试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
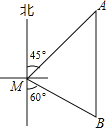
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
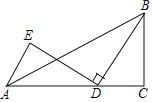
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )

A.2mB.4mC.![]() mD.
mD.![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
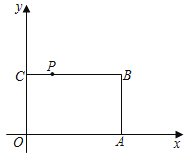
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边O在x轴上,OC在y轴上,OA=6,OC=4,PC=![]() BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
A.(3![]() ,
,![]() )B.(2,﹣1)
)B.(2,﹣1)
C.(![]() ,﹣3
,﹣3![]() )D.(﹣1,2)
)D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
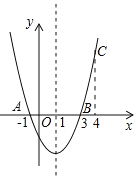
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
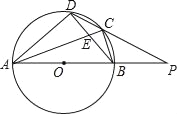
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com