
【题目】在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.
(1)操作发现:
若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是 , ;
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.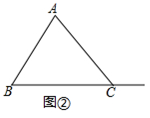
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3 ![]() 时,请直接写出线段CF的长的最大值是
时,请直接写出线段CF的长的最大值是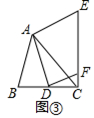
【答案】
(1)CE=BD;CE⊥BD
(2)
解:(1)中的结论仍然成立.理由如下:
如图2,
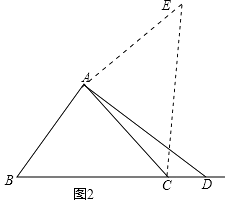
∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,
∵AB=AC,∠BAC=90°
∴∠CAE=∠BAD,
∴△ACE≌△ABD,
∴CE=BD,∠ACE=∠B,
∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
(3)45;![]()
【解析】解:(1)①∵AB=AC,∠BAC=90°,
∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD;
故答案为:CE=BD,CE⊥BD;(3)45°; ![]() ;
;
过A作AM⊥BC于M,过E点作EN垂直于MA延长线于N,如图3,
∵线段AD绕点A逆时针旋转90°得到AE,
∴∠DAE=90°,AD=AE,
∴∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,
∴NE=AM,
∵CE⊥BD,即CE⊥MC,∴∠NEC=90°,
∴四边形MCEN为矩形,
∴NE=MC,∴AM=MC,
∴∠ACB=45°,
∵四边形MCEN为矩形,
∴Rt△AMD∽Rt△DCF,
∴ ![]() =
= ![]() ,设DC=x,
,设DC=x,
∵在Rt△AMC中,∠ACB=45°,AC=3 ![]() ,
,
∴AM=CM=3,MD=3﹣x,∴ ![]() =
= ![]() ,
,
∴CF=﹣ ![]() x2+x=﹣
x2+x=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时有最大值,最大值为
时有最大值,最大值为 ![]() .
.
故答案为:45°, ![]() .
.
(1)线段AD绕点A逆时针旋转90°得到AE,根据旋转的性质得到AD=AE,∠BAD=∠CAE,得到△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.(2)证明的方法与(1)一样.(3)过A作AM⊥BC于M,EN⊥AM于N,根据旋转的性质得到∠DAE=90°,AD=AE,利用等角的余角相等得到∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA,则NE=MA,由于∠ACB=45°,则AM=MC,所以MC=NE,易得四边形MCEN为矩形,得到∠DCF=90°,
由此得到Rt△AMD∽Rt△DCF,得 ![]() ,设DC=x,而∠ACB=45°,AC=
,设DC=x,而∠ACB=45°,AC= ![]() ,得AM=CM=3,MD=3﹣x,利用相似比可得到CF=﹣
,得AM=CM=3,MD=3﹣x,利用相似比可得到CF=﹣ ![]() x2+1,再利用二次函数即可求得CF的最大值.
x2+1,再利用二次函数即可求得CF的最大值.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.

(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
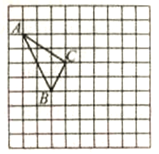
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次为A1,A2,A3,A4,A5,…,则顶点A55的坐标是( )

A. (13,13) B. (-13,-13) C. (-14,-14) D. (14,14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.
(1)求A、B两种型号的轿车每辆分别多少元?
(2)若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面对话,可知懒羊羊所买的笔和笔记本的;
价格分别为( )
喜羊羊:懒羊羊,你上周买的笔和笔记本的价格是多少啊?
懒羊羊:哦,我忘了,只记得先后买了两次,第一次买了5支笔和10本笔记本共花了42元钱,第二次买了10支笔和5本笔记本共花了30元钱。
A. 0.8元/支,2.6元/本 B. 0.8元/支,3.6元/本
C. 1.2元/支,3.6元/本 D. 1.6元/支,3.2元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组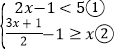
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A.2
B.2 ![]()
C.2 ![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是( )
A.(2n﹣1 , 2n﹣1)
B.(2n , 2n﹣1)
C.(2n﹣1 , 2n+1)
D.(2n﹣1 , 2n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com