
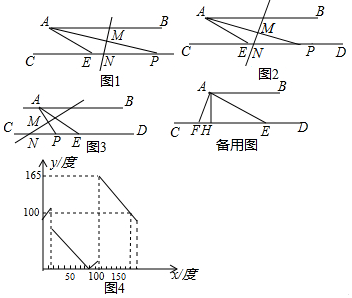
分析 (1)当x=12时,根据三角形外角的性质可:∠MNE=90°+12°=102°;
当x=50°,根据直角三角形两锐角互余可得结论;
(2)由图象直接得出结论;
(3)分两种情况:①P在E的左侧,②P在E的右侧,根据平行线的性质和中垂线的性质可得结论;
(4)如图7,根据三角形外角和为360°列式可得结论.
解答 解:(1)如图2,∵AB∥CD,
∴∠BAP=∠APN=x°,
∵MN⊥AP,
∴∠PMN=90°,
∴∠MNE=∠PMN+∠APN=90°+x°,
当x=12时,∠MNE=(90+12)°=102°;
即y=102°,
如图3中,当x=50时,∠APN=50°,
∴y=∠MNE=90°-x°=90°-50°=40°,
故答案为:102°,40°;
(2)如图2,当0<x<30时,y=90+x,
此时,y=100时,90+x=100,x=10,
由图4可知:y=100时,还有x=170,
∴当y=100时,x=10或170,
故答案为:10或170;
(3)①P在E的左侧时,当N与E重合时,如图5,∠BAE=∠AEP=30°,
∵MN是AP的中垂线,
∴AE=PE,
∴∠AEM=∠PEM=15°,
∴∠EAP=90°-15°=75°,
∴∠BAP=x=30°+75°=105°,
②P在E的右侧时,当N与E重合时,如图6,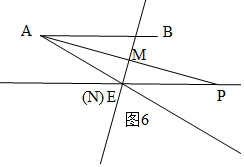
∵AB∥CD,
∴∠BAP=∠APE=x,
同理得:AE=PE,
∴∠EAM=∠EPM=x,
∵∠BAE=30°,
∴∠BAP=x=∠EAP=$\frac{1}{2}∠BAE$=15°,
综上所述,当x=15或105时,点N与点E重合;
故答案为:15或105;
(4)当x>105时,如图7,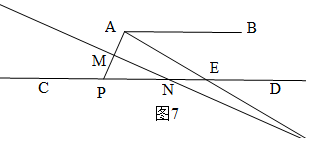
∵AB∥CD,
∴∠APC=∠BAP=x,
∵∠APC+∠MNE+∠AMN=360°,∠AMN=90°,
∴∠APC+∠MNE=360°-90°=270°,
∴∠MNE=270°-∠APC=270°-∠BAP,
即y=270-x.
点评 本题考查了平行线的性质、等腰三角形三线合一的性质、中垂线的性质、三角形外角定理、一次函数,属于动点问题的函数图象,有难度,并采用了分类讨论,数形结合思想解决问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )| A. | $\frac{125}{12}$ | B. | $\frac{125}{24}$ | C. | 40 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 充值金额(元) | 充值后卡内金额(元) | |
| 以前 | 即日起 | |
| 200 | 200 | 250 |
| 500 | 600 | 650 |
| 1000 | 1200 | 1400 |
| 购买服装的标价(元) | 折扣 | |
| 以前 | 即日起 | |
| 1-100 | 不打折 | 不打折 |
| 100-300 | 不打折 | 9折 |
| 300-400 | 9折 | 8折 |
| 不低于400 | 8折 | 7折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com