
(1)求EH和HF的长;
(2)求BC的长.
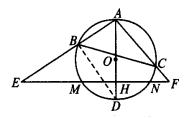
| (1)依题意,及一元二次方程根与系数关系,
得D=[-(k+2)]2-4×4k>0, ① EH+HF=k+2, ② EH·HF=4k>0, ③ 又EH-HF=2. ④ 由②、③、④得k=12. 当k=12时,①成立,把k=12代入原方程解得x1=8,x2=6. ∴ EH=8,HF=6. (2)连结BD.∴ ∠ADB=∠a. ∵ ∴ AD⊥EF,即∠AHE=∠AHF=90°. ∴ ∠E=∠ADB=∠a. 在Rt△AEH中,tanE= 又EH=8,∴ AH=6. 由勾股定理,得AE=10,AF= ∵ tanADB= 设AB=3 m,则BD=4 m. ∴ AD=5 m. ∵ H是OD的中点,∴ AD=8,AB= ∵ ∠E=∠a,∠BAC=∠FAE, ∴ △ABC∽△AFE.∴ ∴ BC=
|


科目:初中数学 来源: 题型:
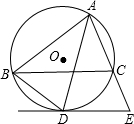 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com