
 (2013•绍兴)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
(2013•绍兴)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )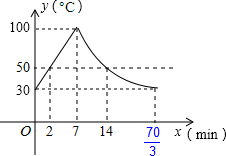 解:∵开机加热时每分钟上升10℃,
解:∵开机加热时每分钟上升10℃,| k |
| x |
| k |
| x |
| 700 |
| x |
| 700 |
| x |
| 70 |
| 3 |
| 700 |
| x |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 40 |
| 3 |
| 70 |
| 3 |
| 70 |
| 3 |
| 25 |
| 3 |
| 70 |
| 3 |


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
 (2013•绍兴模拟)小刚在纸上画了一个面积为6分米2的正六边形,然后连接相隔一点的两点得到如图所示的对称图案,他发现中间也出现了一个正六边形,则中间的正六边形的面积是
(2013•绍兴模拟)小刚在纸上画了一个面积为6分米2的正六边形,然后连接相隔一点的两点得到如图所示的对称图案,他发现中间也出现了一个正六边形,则中间的正六边形的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•绍兴模拟)如图,在平面直角坐标系中,A(1,0)、B(5,0)、C(6,3)、D(0,3),点P为线段CD上一点,且∠APB=45°,则点P的坐标为
(2013•绍兴模拟)如图,在平面直角坐标系中,A(1,0)、B(5,0)、C(6,3)、D(0,3),点P为线段CD上一点,且∠APB=45°,则点P的坐标为| 7 |
| 7 |
| 7 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•绍兴模拟)已知M、N为双曲线y=
(2013•绍兴模拟)已知M、N为双曲线y=| 4 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com