
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+ ![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.
【答案】
(1)1;2
(2)
解:当 ![]() 时,y有最小值,即
时,y有最小值,即 ![]() 时,
时, ![]()
【解析】(1)解:①当y=4 ![]() 时,x=4,
时,x=4,
∴m=4;∴函数y=x+ ![]() (x>0)的图象如图.
(x>0)的图象如图.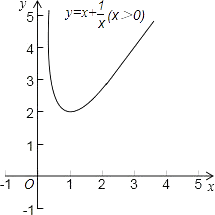
②当0<x<1时,y随x增大而减小;当x>1时,y随x增大而增大;当x=1时函数y=x+ ![]() (x>0)的最小值为2.
(x>0)的最小值为2.
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程指:含有一个未知数,且未知数的最高次数为2的等式,求一元二次方程![]() 解的方法如下:第一步:先将等式左边关于x的项进行配方,
解的方法如下:第一步:先将等式左边关于x的项进行配方, ![]() ,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,
,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,![]() ;第三步:根据平方的逆运算,求出
;第三步:根据平方的逆运算,求出![]() 或-3;第四步:求出
或-3;第四步:求出![]() .类比上述求一元二次方程根的方法,(1)解一元二次方程:
.类比上述求一元二次方程根的方法,(1)解一元二次方程:![]() ;
;
(2)求代数式![]() 的最小值;
的最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
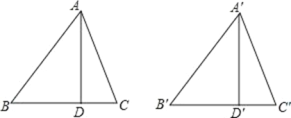
【题目】如图,锐角三角形 ABC 和锐角三角形 A'B'C'中,AD、A'D'分别是边 BC、B'C'上的高,且AB=A'B',AD=A'D'.要使△ABC≌△A'B'C',则应补充条件:________(填写一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义: 如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2). ①当t=2时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y= ![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
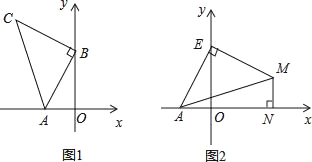
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC绕点O按顺时针方向旋转90°后的△A2B2C2;
(2)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com