

 >0可得到b的取值,然后即可判定A是否正确;由于图象与y轴有两个交点可以推出b2-4ac>0,由此可以判定B正确;由0<-
>0可得到b的取值,然后即可判定A是否正确;由于图象与y轴有两个交点可以推出b2-4ac>0,由此可以判定B正确;由0<- <1可得-2a<b<0,a<0,由此可以判定C正确;用排除法可知D错误.
<1可得-2a<b<0,a<0,由此可以判定C正确;用排除法可知D错误. >0,
>0, <1可得-2a<b<0,a>0,
<1可得-2a<b<0,a>0,

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
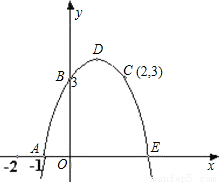
查看答案和解析>>
科目:初中数学 来源:2002年湖北省黄冈市中考数学试卷(解析版) 题型:解答题
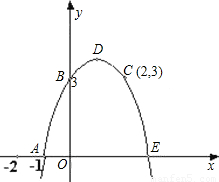
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《图形的相似》(05)(解析版) 题型:解答题
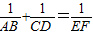 成立(不要求考生证明).
成立(不要求考生证明). 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;

查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(01)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com