
【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.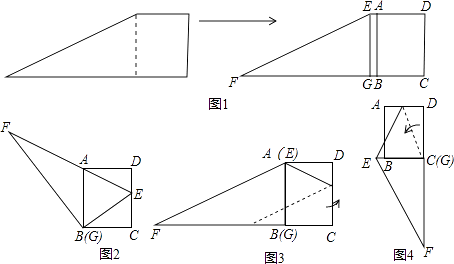
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度;
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红.
【答案】
(1)
解:∵BE=AB=15,
在直角△BCE中,
CE= ![]() =
= ![]() =9
=9
∴DE=6,
∵∠EAD+∠BAE=90°,∠BAE=∠BEF,
∴∠EAD+∠BEF=90°,
∵∠BEF+∠F=90°,
∴∠EAD=∠F
∵∠ADE=∠FBE
∴△ADE∽△FBE,
∴ ![]() ,
,
![]() ,
,
∴BF=30
(2)
解:①如图1,将矩形ABCD和直角△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,
∵Rt△F′HN∽Rt△F′EG,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
解得:HN=3,
∴S△AMH= ![]() AMMH=
AMMH= ![]() ×12×24=144;
×12×24=144;
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,
∵Rt△GBE∽Rt△GB′C′,
∴ ![]() ,即
,即 ![]() ,解得:GB′=24,
,解得:GB′=24,
∴S△B′C′G= ![]() B′C′B′G=
B′C′B′G= ![]() ×12×24=144,
×12×24=144,
∴按照两种包裹方法的未包裹面积相等.
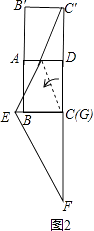
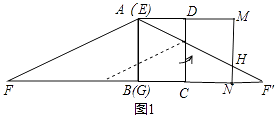
【解析】(1)先证明△ADE∽△FBE,利用相似的性质得BF;(2)①利用相似三角形的判定,证明Rt△F′HN∽Rt△F′EG,利用相似三角形的性质,求得HN,利用三角形的面积公式得结果;②利用相似三角形的判定,证明Rt△F′HN∽Rt△F′EG,利用相似三角形的性质,求得HN,利用三角形的面积公式得结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD的四个顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).
(1)试计算四边形ABCD的面积;
(2)若将该四边形各顶点的横坐标都加2,纵坐标都加3,其面积怎么变化?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点E在AC的延长线上,有下列条件∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 4,3 C. 4,
B. 4,3 C. 4,![]() D. 2,1
D. 2,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个长方形的三个顶点坐标分别为(﹣2,﹣2),(﹣2,3),(5,﹣2),则第四个顶点的坐标( )
A. (5,3) B. (3,5) C. (7,3) D. (3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 ( )
①2∠DCF=∠BCD; ②EF=CF; ③S△BEC=2S△CEF; ④∠DFE=3∠AEF.

A. ①②③④ B. ①②④ C. ①② D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com