
����Ŀ����ѧ��С������ٴ�ҵ������һ�ֽ���Ϊ![]() Ԫ/��������ܣ����۹����з��֣�ÿ���������٣����������۵���
Ԫ/��������ܣ����۹����з��֣�ÿ���������٣����������۵���![]() ��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����
��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����![]()
![]() ���С����Ҫÿ�ܻ��
���С����Ҫÿ�ܻ��![]() Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ��
Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ��
![]() ��С��ÿ�ܻ������Ϊ
��С��ÿ�ܻ������Ϊ![]() ��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�ܿɻ�����������������Ƕ��٣�
��Ԫ���������۵��۶�Ϊ����Ԫʱ��ÿ�ܿɻ�����������������Ƕ��٣�
![]() ��������ܵ����۵��۲��ø���
��������ܵ����۵��۲��ø���![]() Ԫ�����С����Ҫÿ�ܻ�õ�������
Ԫ�����С����Ҫÿ�ܻ�õ�������![]() Ԫ����ô�������۵���Ӧ��Ϊ���٣�
Ԫ����ô�������۵���Ӧ��Ϊ���٣�
���𰸡�(1)���۵���Ӧ��Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��(2) ���ۼ�Ϊ
Ԫ��(2) ���ۼ�Ϊ![]() Ԫ/̨ʱ���������Ϊ
Ԫ/̨ʱ���������Ϊ![]() Ԫ��(3) �������۵���Ӧ��Ϊ
Ԫ��(3) �������۵���Ӧ��Ϊ![]() Ԫ��
Ԫ��![]() Ԫ֮�䣮
Ԫ֮�䣮
��������
��1��������=������ÿ���������赥�۶�ΪxԪ��w=����2x+100����x��20��=��2x2+140x��2000����w=400�����x���ɣ���2����w�Ľ���ʽ��Ϊ����ʽ��⼴�ɣ���3������������ͼ����ͼ��д��x�ķ�Χ����.
(1) w=����2x+100����x��20��=��2x2+140x��2000��
��w=400����2x2+140x��2000=400��
���x1=30��x2=40��
���۵���Ӧ��Ϊ30Ԫ��40Ԫ��
(2)w=(x��20)(��2x+100)=��2x2+140x��2000=��2(x��35)2+450��
�൱x=35ʱ��wȡ�����ֵ�����ֵΪ450Ԫ��
(3)����w��ͼ��
��y=0��2x2+140x��2000=0��
���x1=20��x2=50��
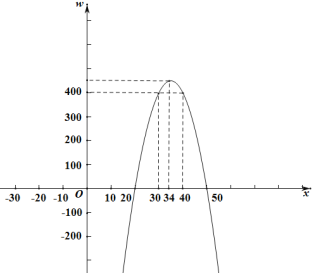
��ͼ���ѵó���30��x��34��
�������۵���Ӧ����30Ԫ��34Ԫ֮��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
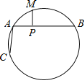
����Ŀ����֪![]() �ǻ�
�ǻ�![]() ���е㣬
���е㣬![]() ��ֱ����
��ֱ����![]() ��
��![]() ������
������![]() �ij���Ϊ
�ij���Ϊ![]() ���߶�
���߶�![]() �ij�����
�ij�����![]() ����ô�߶�
����ô�߶�![]() �ij�����________�����ú���
�ij�����________�����ú���![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�����Ű�����ÿǧ��2Ԫ�ļ۸�ij��ˮ������ǧ�ˣ�����һ���ֺ����г����齵�����ۣ����۶�y (Ԫ)��������x (ǧ��)֮��Ĺ�ϵ��ͼ��ʾ.

(1)�龳�еı�����_______________.
(2)�ۺ����۶�y (Ԫ)��������x (ǧ��)֮��ĺ�������ʽ;
(3)��������Ϊ����ǧ��ʱ���Ű������۴���ˮ��������Ϊ150Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮
��1��д����������������⣻
��2���ж����������ٲ�˵��������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������Ϊ36���ĵ��������γ�Ϊ��ǻƽ������Σ����ĵ�����֮��Ϊ![]() ��0.618����Ϊk.�ܴ����������꼶��ѧ������̽����Ϊ36���ĵ��������Σ�Ҳ�ƶ۽ǻƽ������Σ���ͼ2��
��0.618����Ϊk.�ܴ����������꼶��ѧ������̽����Ϊ36���ĵ��������Σ�Ҳ�ƶ۽ǻƽ������Σ���ͼ2��
(1)��ͼ1��ͼ2�У���DE=BC����֤��EF=AB��
(2)��۽ǻƽ������ε������ı�ֵ(�ú�k��ʽ�ӱ�ʾ)��
(3)��ͼ3���ڶ۽ǻƽ�������ABC�У�AD��DE���ηָ���۽ǻƽ���������ADC����ADE����AB��1������ABC����ADC����ADE�ֱ�Ϊ��1��2��3���۽ǻƽ������Σ��Դ����ƣ����2020���۽ǻƽ������ε��ܳ�(�ú�k��ʽ�ӱ�ʾ).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B������ֱ�Ϊ��1��4���ͣ�4��4����������y=a��x-m��2+n�Ķ������߶�AB���˶�����x�ύ��C��D���㣨C��D����ࣩ����C�ĺ�������СֵΪ-3�����D�ĺ��������ֵΪ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������![]() ��B����2��6����C��2��2�����㣮
��B����2��6����C��2��2�����㣮

��1�����������ߵĽ���ʽ��
��2���������߶���ΪD�����BCD�������
��3����ֱ��![]() ����ƽ��b����λ���õ�ֱ���������߶�BDC�������˵�B��C���������������㣬��b��ȡֵ��Χ��
����ƽ��b����λ���õ�ֱ���������߶�BDC�������˵�B��C���������������㣬��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һԲ�����Ź���Բ��Ϊ![]() �����ŵ�ˮ����
�����ŵ�ˮ����![]() �ף��Ź���ˮ������߶�
�ף��Ź���ˮ������߶�![]() Ϊ
Ϊ![]() �ף���
�ף���

![]() �Ź��İ뾶��
�Ź��İ뾶��
![]() ��ˮ�����Ǻ�ˮ����Ϊ
��ˮ�����Ǻ�ˮ����Ϊ![]() �ף���ˮ�����ǵĸ߶�Ϊ________�ף�
�ף���ˮ�����ǵĸ߶�Ϊ________�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ1�ĵȱ�![]() �ı�
�ı�![]() ��һ��
��һ��![]() ����
����![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ʱ������
ʱ������![]() ��
��![]() ����
����![]() ����
����![]() �ij�Ϊ______.
�ij�Ϊ______.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com