
【题目】如图1,已知线段AB=16cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.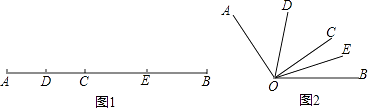
(1)若点C恰为AB的中点,求DE的长;
(2)若AC=6cm,求DE的长;
(3)试说明不论AC取何值(不超过16cm),DE的长不变;
(4)知识迁移:如图2,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=65°与射线OC的位置无关.
【答案】
(1)解:∵点C恰为AB的中点,
∴AC=BC= ![]() AB=8cm,
AB=8cm,
∵点D、E分别是AC和BC的中点,
∴DC= ![]() AC=4cm,CE=
AC=4cm,CE= ![]() BC=4cm,
BC=4cm,
∴DE=8cm
(2)解:∵AB=16cm,AC=6cm,
∴BC=10cm,
由(1)得,DC= ![]() AC=3cm,CE=
AC=3cm,CE= ![]() CB=5cm,
CB=5cm,
∴DE=8cm
(3)解:∵点D、E分别是AC和BC的中点,
∴DC= ![]() AC,CE=
AC,CE= ![]() BC,
BC,
∴DE= ![]() (AC+BC)=
(AC+BC)= ![]() AB,
AB,
∴不论AC取何值(不超过16cm),DE的长不变
(4)解:∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC= ![]() ∠AOC,∠EOC=
∠AOC,∠EOC= ![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOC= ![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=65°,
∠AOB=65°,
∴∠DOE=65°与射线OC的位置无关
【解析】(1)由点C恰为AB的中点,得到AC=BC的值,再由点D、E分别是AC和BC的中点,求出DE的值;(2)由(1)得,DC=![]() AC的值,CE=
AC的值,CE=![]() CB的值,得到DE的值;(3)由点D、E分别是AC和BC的中点,得到不论AC取何值(不超过16cm),DE的长不变;(4)由OD、OE分别平分∠AOC和∠BOC,根据角平分线定义,得到∠DOE=∠DOC+∠EOC=
CB的值,得到DE的值;(3)由点D、E分别是AC和BC的中点,得到不论AC取何值(不超过16cm),DE的长不变;(4)由OD、OE分别平分∠AOC和∠BOC,根据角平分线定义,得到∠DOE=∠DOC+∠EOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,得到∠DOE=65°与射线OC的位置无关.
∠AOB,得到∠DOE=65°与射线OC的位置无关.


科目:初中数学 来源: 题型:
【题目】为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,扩大知识源,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动,活动前对本校学生进行了“你最喜欢的图书类型(只写一项)”的随机抽样调查,相关数据统计如下:
请根据以上信息解答下列问题: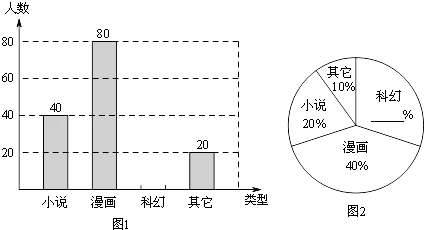
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;并求出扇形统计图中小说所对应的圆心角度数.
(3)已知该校共有学生800人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
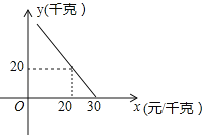
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )
A.0.3×106
B.3×105
C.3×106
D.30×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( ) 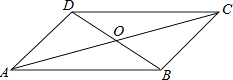
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com