
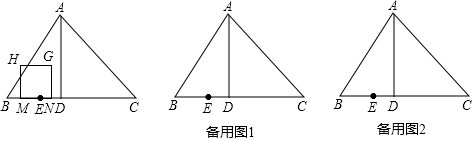
分析 (1)如图1中,当H在AB上时,易知BM=3t,HM=4t,根据HM=MN列出方程即可解决问题;如图2中,当H在AC上时,根据HM=MN列出方程即可解决问题;
(2)分四种情形列出方程即可①如图3中,当0<t≤$\frac{2}{3}$时,重叠部分是五边形MNGPK.②如图4中,当$\frac{2}{3}$<t≤2时,重叠部分是正方形MNGH.③如图5中,当2<t≤$\frac{18}{5}$时,重叠部分是四边形MNGH.④如图6中,当$\frac{18}{5}$<t≤$\frac{14}{3}$时,重叠部分是五边形MNGKP;
(3)如图7中,设PM为直径的⊙O与AD相切于点K,OK交PN于J.根据OK=$\frac{1}{2}$PM,列出方程即可;
解答 解:(1)如图1中,当H在AB上时,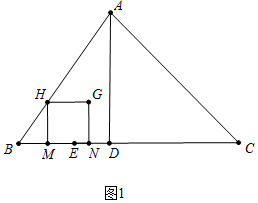
在Rt△ABD中,∵tanB=$\frac{AD}{BD}$=$\frac{4}{3}$,AD=8,
∴BD=6,
在Rt△ACD中,∵∠ACD=45°,
∴AD=DC=8,
易知BM=3t,HM=4t,
∵MN=4-3t+t=4-2t,
∴4t=4-2t,
∴t=$\frac{2}{3}$,
如图2中,当H在AC上时,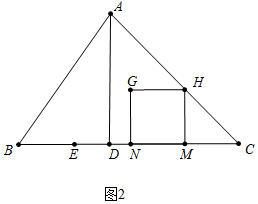
∵HM=CM=MN,
∴14-3t=3t-4-t,
∴t=$\frac{18}{5}$,
故答案为$\frac{2}{3}$s或$\frac{18}{5}$s.
(2)①如图3中,当0<t≤$\frac{2}{3}$时,重叠部分是五边形MNGPK.
S=S正方形MNGH-S△PHK=(4-3t+t)2-$\frac{1}{2}$•[4-2t-4t]•$\frac{3}{4}$[4-2t-4t]=-$\frac{19}{2}$t2+2t+10.
②如图4中,当$\frac{2}{3}$<t≤2时,重叠部分是正方形MNGH.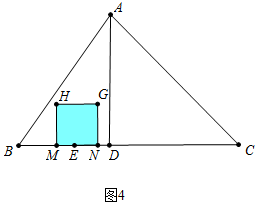
S=(4+t-3t)2=4t2-16t+16.
③如图5中,当2<t≤$\frac{18}{5}$时,重叠部分是四边形MNGH.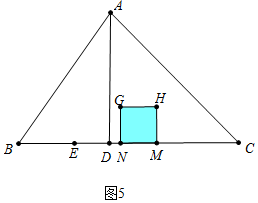
S=(3t-4-t)2=4t2-16t+16.
④如图6中,当$\frac{18}{5}$<t≤$\frac{14}{3}$时,重叠部分是五边形MNGKP.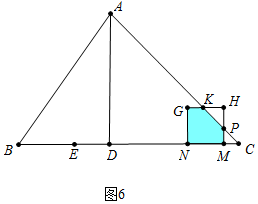
S=S正方形MNGH-S△PHK=(2t-4)2-$\frac{1}{2}$•[(2t-4)-(14-3t)]2=-$\frac{17}{2}$t2+74t-146.
综上所述,S=$\left\{\begin{array}{l}{-\frac{19}{2}{t}^{2}+2t+10}&{(0<t≤\frac{2}{3})}\\{4{t}^{2}-16t+16}&{(\frac{2}{3}<t≤\frac{18}{5})}\\{-\frac{17}{2}{t}^{2}+74t-146}&{(\frac{18}{5}<t≤\frac{14}{3})}\end{array}\right.$.
(3)如图7中,设PM为直径的⊙O与AD相切于点K,OK交PN于J.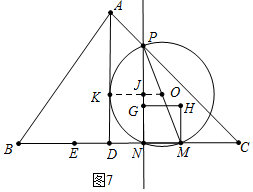
易知:JK=DN=t-2,OJ=$\frac{1}{2}$MN=t-2,PM=$\sqrt{P{N}^{2}+M{N}^{2}}$=$\sqrt{(14-4-t)^{2}+(2t-4)^{2}}$,
∵OK=$\frac{1}{2}$PM,
∴$\frac{1}{2}$$\sqrt{(10-t)^{2}+(2t-4)^{2}}$=t-2+t-2,
解得t=$\frac{14+16\sqrt{3}}{11}$或$\frac{14-16\sqrt{3}}{11}$(舍弃),
∴t=$\frac{14+16\sqrt{3}}{11}$s时,△PMN的外接圆与AD相切.
点评 本题考查几何变换综合题、圆、正方形的性质、等腰直角三角形的性质、锐角三角函数等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com