
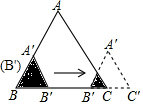
 如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )| A. | 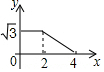 | B. | 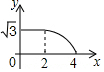 | C. | 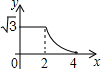 | D. | 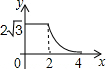 |
分析 根据题目提供的条件可以求出函数的解析式,根据解析式判断函数的图象的形状.
解答 解:①x≤2时,两个三角形重叠面积为小三角形的面积,
∴y=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
②当2<x≤4时,重叠三角形的边长为4-x,高为$\frac{\sqrt{3}}{2}$(4-x),
y=$\frac{1}{2}$(4-x)×$\frac{\sqrt{3}}{2}$(4-x)=$\frac{\sqrt{3}}{4}$x2-2$\sqrt{3}$x+4$\sqrt{3}$,
③当x=4时,两个三角形没有重叠的部分,即重叠面积为0,
故选:C.
点评 本题主要考查了动点问题的函数图象,此类题目的图象往往是几个函数的组合体,解题的关键是求出函数关系式.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
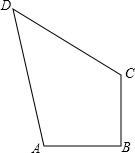 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:
已知函数y=$\frac{4}{|x|}$,小明研究该函数的图象及性质时,列出y与x的几组对应值如下表:| x | … | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | … |
| y | … | 1 | $\frac{4}{3}$ | 2 | 4 | 4 | 2 | $\frac{4}{3}$ | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com