练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知a、b满足等式x=2a2+b2+4，y=2a（b+2），试比较x与y的大小关系．

    分析 根据求差法比较大小即可．

    解答 解：x-y=（2a2+b2+4）-2a（b+2）=2a2+b2+4-2ab-4a=（a2-4a+4）+（a2-2ab+b2）=（a-2）2+（a-b）2，
    ∵（a-2）2≥0，（a-b）2≥0，
    ∴x-y≥0，
    ∴x≥y．

    点评 本题考查因式分解、乘法公式、非负数的性质等知识，解题的关键是学会求差法比较大小，学会利用乘法公式变形，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．若顺次连接四边形的各边中点所得的四边形是菱形，则该四边形一定是（　　）
    A．矩形B．菱形
    C．对角线相等的四边形D．对角线互相垂直的四边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知（x5my2m-2n）3•（2xnyn）3=8x6y15，求（m+n）m-n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．若数轴上表示数x的点在原点的左边，则化简|x|+$\sqrt{{x}^{2}}$的结果是（　　）
    A．2xB．-2xC．0D．x

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．数字a、b在数轴上的位置如图所示，试化简$\sqrt{（b-a）^{2}}$+|2-a|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

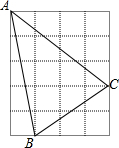    14．阅读：直角三角形具有下列性质，若直角三角形的两直角分别为a，b．斜边为c，则a2+b2=c2，利用这一性质．可求出某些线段的长，如图，正方形网格中，每个小正方形的边长均为1，则BC2=22+32，即BC=$\sqrt{2^2+3^2}$=$\sqrt{13}$，因3$＜\sqrt{13}＜$4，所以线段BC的长是无理数，请你利用以上阅读材料，判断图中线段AC、AB的长是有理数还是无理数，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）（x-y）（x2+xy+y2）
    （2）${（-6{x^2}y）^2}•（\frac{1}{3}{x^3}{y^2}-\frac{2}{9}{x^2}y+x）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知（x2+mx+n）（x2-3x+2）中，不含x3项和x项，求m，n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）（x+y）（x2-xy+y2）
    （2）-12x2y•（$\frac{1}{3}$x3y2-$\frac{3}{4}{x}^{2}y$+$\frac{1}{6}$）

    查看答案和解析>>

    同步练习册答案