
如图,△ABC是一等腰三角形铁板,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一个矩形零件DEFG,使EF在边BC上,若D、G分别在边AB、AC上.
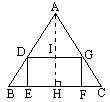
(1)设EF=x cm,S矩形DEFG=y cm2,试求y关于x的函数关系式;(2)当x为多少时,矩形DEFG的面积最大?
|
解答: (1)如图,过A点作AH⊥BC,垂足为H,交DG于I.则AH=
∵ DG∥BC,∴△ADG∽△ABC,∴又 EF=DG,AI=AH-DE,∴ ∴ y=EF·DE=x(16-(2)y=- 当 x=12时,y=96,这时是矩形面积的最大值.分析:由于知形 DEFG的面积为长×宽,当EF=x时,关键是要用x表示出DE来.作 AH⊥BC,利用勾股定理可以求出AH的长,再利用相似三角形的比例关系求出AI的长.从而可求出IH=DE.当矩形 DEFG的面积y是x的二次函数时,可以求出面积的最大值. |


科目:初中数学 来源: 题型:
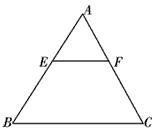
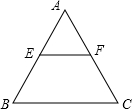 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
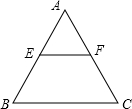 已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.查看答案和解析>>
科目:初中数学 来源: 题型:
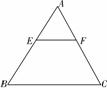
已知:如图,一等边三角形ABC纸片的边长为2a,E是AB边上一动点,(点E与点A、B不重合),过点E作EF∥BC,交AC于点F,设EF=x.
(1)用x的代数式表示△AEF的面积;
(2)将△AEF沿EF折叠,折叠后与四边形BCFE重叠部分的面积为y,求出y关于x的函数关系式,并写出自变量x的取值范围.
 |
查看答案和解析>>
科目:初中数学 来源:北京模拟题 题型:解答题
查看答案和解析>>
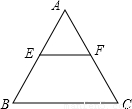
科目:初中数学 来源:2009年北京市通州区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com