
【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y. 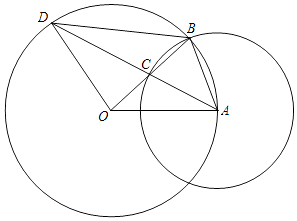
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
【答案】
(1)解:在⊙O与⊙A中,
∵OA=OB,AB=AC,
∴∠ACB=∠ABC=∠OAB,
∴△ABC∽△OAB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BC= ![]() x2,
x2,
∵OC=OB﹣BC,
∴y关于x的函数解析式y=2﹣ ![]() x2,
x2,
定义域为0<x<2.
(2)解:①当OD∥A B时,
∴ ![]() =
= ![]() ,
,
∴  =
= ![]() ,
,
整理得x2+2x﹣4=0,
∴x=﹣1 ![]() (负值舍去),
(负值舍去),
∴AB= ![]() ,这时AB≠OD,符合题意.
,这时AB≠OD,符合题意.
∴OC=2﹣ ![]() x2=2﹣
x2=2﹣ ![]() (
( ![]() ﹣1)2=
﹣1)2= ![]() ﹣1.
﹣1.
②当BD∥OA时,设∠ODA=α,
∵BD∥OA,OA=OD,
∴∠BDA=∠OAD=∠ODA=α,
又∵OB=OD,∴∠BOA=∠OBD=∠ODB=2α,
∵AB=AC,OA=OB,
∴∠OAB=∠ABC=∠ACB=∠COA+∠CAO=3α,
∵∠AOB+∠OAB+∠OBA=180°,
∴2α+3α+3α=180°,
∴α=22.5°,∠BOA=45°,
∴∠ODB=∠OBD=45°,∠BOD=90°,
∴BD=2 ![]() ,
,
∵BD∥OA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴y=2 ![]() ﹣2.OC=2
﹣2.OC=2 ![]() ﹣2,
﹣2,
由于BD≠OA,OC=2 ![]() ﹣2符合题意.
﹣2符合题意.
∴当四边形ABDO是梯形时,线段OC的长为 ![]() ﹣1或2
﹣1或2 ![]() ﹣2.
﹣2.

【解析】(1)由△ABC∽△OAB,推出 ![]() =
= ![]() ,可得
,可得 ![]() =
= ![]() ,推出BC=
,推出BC= ![]() x2,由OC=OB﹣BC,可得y关于x的函数解析式y=2﹣
x2,由OC=OB﹣BC,可得y关于x的函数解析式y=2﹣ ![]() x2;(2)分两种情形讨论①当OD∥A B时,②当BD∥OA时,分别想办法构建方程解决问题;
x2;(2)分两种情形讨论①当OD∥A B时,②当BD∥OA时,分别想办法构建方程解决问题;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE= ![]() AB;③S△ADE=
AB;③S△ADE= ![]() S△ABC . 正确的有( )
S△ABC . 正确的有( )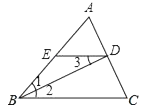
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB= ![]() πcm2;②
πcm2;② ![]() ;③∠ACB=20°;④∠ADB=140°.错误的有( )
;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.
(1)若∠CAE=∠B+30°,求∠B的大小;
(2)若AC=3,AB=5,求△AEB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中,装有红、黄、白、黑四种只有颜色不同的小球,其中红色小球有30个,黄、白、黑色小球的数目相同.为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,放回后再次搅匀…多次试验发现摸到红球的频率是 ![]() ,则估计黄色小球的数目是 .
,则估计黄色小球的数目是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com