
【题目】泰州梅兰芳公园开放后,前往参观的人非常多.5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 ;
(2)求表中a、b、c的值,并请补全频数分布直方图;
(3)在调查人数里,等候时间少于40min的有 人;
(4)此次调查中,中位数所在的时间段是 ~ min.|X

【答案】(1)填抽样调查或抽查;
(2)∵a=1-0.200-0.250-0.125-0.075=0.350;
b=8÷0.200×0.125=5;
c=8÷0.200=40;
频数分布直方图如图所示.

(3)依题意得在调查人数里,等候时间少于40min的有8+14+10=32人;
故填32.
(4)∵总人数为40人,
∴中位数所在的时间段是20~30.
故填20,30.
【解析】(1)由于前往参观的人非常多,5月中旬的一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,由此即可判断调查方式;
(2)首先根据已知的一组数据可以求出接受调查的总人数c,然后乘以频率即可求出b,利用所有频率之和为1即可求出a,然后就可以补全频率分布直方图;
(3)根据表格知道被调查人数里,等候时间少于40min的有第一、二、三小组,利用表格数据即可求出等候时间少于40min的人数;
(4)由于知道总人数为40人,根据中位数的定义就可以知道中位数落在哪个小组。


科目:初中数学 来源: 题型:
【题目】如图,O为数轴原点,A,B两点分别对应﹣3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为__________.若以A为圆心,CO长为半径画弧交数轴于点N,则点N对应的实数为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP’C, 那么是否存在点P,使四边形POP’C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有4个白球和3个黑球,它们除了颜色外都相同,随机从中摸出2个球,属于不可能事件的是( )
A.摸到2个白球
B.摸到2个黑球
C.摸到1个白球,1个黑球
D.摸到1个黑球,1个红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地正面朝上;③任取两个负数,其积大于0;④长分别为3、5、9厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知7+![]() 和7-
和7- ![]() 的小数部分分别为a,b,试求代数式ab-a+4b-3的值
的小数部分分别为a,b,试求代数式ab-a+4b-3的值
(2)设a,b,c都是实数,且满足![]() ,
, ![]() ,求式子
,求式子![]() 的算术平方根.
的算术平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)如图2,过A、E、F三点作圆,若EC=4,∠CEF=15°,求AE的长.
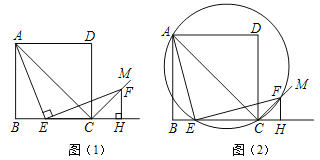
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五张正面分别写有数字﹣2,﹣1,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第二象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com