24
分析:由勾股定理求出BC上的高AN为8cm,求出AO=ON=4cm,求出MN=DE MN∥DE,求出MN与DE间的距离是4cm,求出△MNO和△DEO的高均为cm2,求出阴影部分面积即可.
解答:
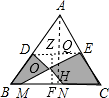
解:连接DE,过A作AH⊥BC于H,过O作ZF⊥BC于F,交DE于Z,
∵AB=AC=10cm,AH⊥BC,BC=12cm,
∴BH=CH=6cm,
∵AB=AC=10cm,
由勾股定理得:AH=8cm,
∵D、E分别是AB和AC中点,
∴DE=

BC=6cm,DE∥BC,
∴DE和MN间的距离是4cm,
∵MN=6cm,BC=12cm,
∴MN=DE,MN∥DE,
∴∠DEO=∠NMO,
在△DEO和△NMO中,
∵
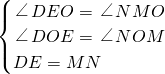
,
∴△DEO≌△NMO(AAS),
∴DO=NO,
∵DE∥MN,
∴△DZO∽△NFO,
∴

=

,
∵DO=ON,
∴ZO=OF=

ZF=2cm,
∴阴影部分的面积是:
S
梯形DECB-S
△DOE-S
△OMN=

×(DE+BC)×FZ-

×DE×OZ-

×MN×OF
=

×(6+12)×4-

×6×2-

×6×2
=24(cm
2).
故答案为:24.
点评:本题考查了相似三角形的性质和判定,三角形的面积,等腰三角形的性质,勾股定理,三角形的中位线定理等知识点的综合运用.

 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为________cm2.
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为________cm2.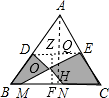
 BC=6cm,DE∥BC,
BC=6cm,DE∥BC,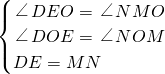 ,
, =
= ,
, ZF=2cm,
ZF=2cm, ×(DE+BC)×FZ-
×(DE+BC)×FZ- ×DE×OZ-
×DE×OZ- ×MN×OF
×MN×OF ×(6+12)×4-
×(6+12)×4- ×6×2-
×6×2- ×6×2
×6×2

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为