
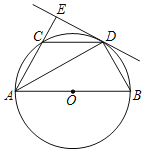
【题目】如图,AB是⊙O的直径,C点在⊙O上,AD平分∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD.
(1)求证:直线DE是⊙O的切线;
(2)若直径AB=6,填空:
①当AD= 时,四边形ACDO是菱形;
②过D作DH⊥AB,垂足为H,当AD= 时,四边形AHDE是正方形.
【答案】(1)证明见解析;(2)①3![]() ②3
②3![]()
【解析】
(1)连接![]() ,根据
,根据![]() 平分
平分![]() ,和
,和![]() ,可证明
,可证明![]() ,再根据
,再根据![]() 即可证明直线
即可证明直线![]() 是
是![]() 的切线;
的切线;
(2)①根据四边形![]() 是菱形,可得
是菱形,可得![]() ,得
,得![]() ,进而可求
,进而可求![]() 的长;
的长;
②当![]() ,即
,即![]() 与
与![]() 重合时,四边形
重合时,四边形![]() 是正方形,根据勾股定理即可得
是正方形,根据勾股定理即可得![]() 的长.
的长.
(1)证明:如图,连接OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴AC∥OD,
∵DE⊥AE,
∴∠AED=90°,
∴∠ODE=90°,
∴DE⊥OD,OD是⊙O的半径,
∴直线DE是⊙O的切线;
(2)解: ①当![]() 时,四边形
时,四边形![]() 是菱形,
是菱形,
理由:四边形ACDO是菱形时,OD=CD=BD=OB,
∴∠DBA=60°,
∵AB是⊙O的直径,
∴∠ADB=90°,
![]() .
.
![]() 当
当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
故答案为:![]() ;
;
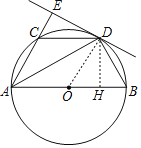
②过D作DH⊥AB,垂足为H,当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
理由:当DH⊥AB,即DH与DO重合时,四边形AHDE是正方形,
由勾股定理,得![]() .
.
![]() 当
当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
故答案为:![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
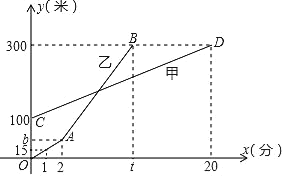
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
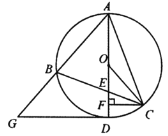
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
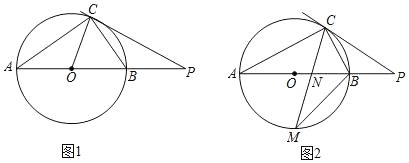
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
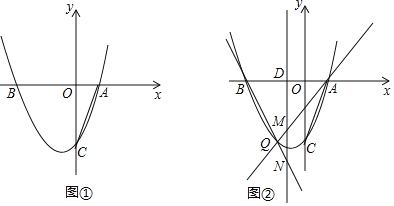
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
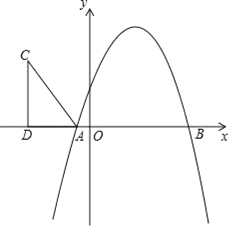
【题目】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
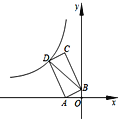
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次初中生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
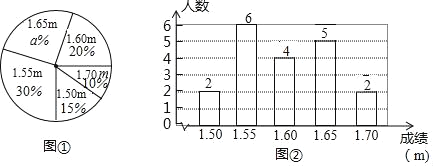
(Ⅰ)图①中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数(结果保留小数点后两位);
(Ⅲ)根据这组初赛成绩,由高到低确定7人进入复赛,请直接写出初赛成绩为1.60m的运动员能否进入复赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com