
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.

(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据圆的对称性可得∠ACD=∠BCD,根据等腰三角形的性质可得CD⊥AB,由EF//AB可得∠CDF=∠CGB=90°,即可得答案;(2)先证明△BCD∽△BDF,利用相似三角形的性质可知:![]() ,利用BC=AC即可求证BD2=ACBF.
,利用BC=AC即可求证BD2=ACBF.
(1)∵AC=BC,CD是圆的直径,
∴由圆的对称性可知:∠ACD=∠BCD,
∴CD⊥AB,
∵AB∥EF,
∴∠CDF=∠CGB=90°,
∵OD是圆的半径,
∴EF是⊙O的切线;
(2)∵∠BDF+∠CDB=∠CDB+∠C=90°,
∴∠BDF=∠CDB,
∴△BCD∽△BDF,
∴![]() ,
,
∴BD2=BCBD,
∵BC=AC,
∴BD2=ACBF.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.

(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
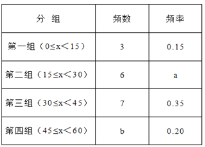
【题目】在大课间活动中,体育老师随机抽取了九年级甲、乙两班部分女生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和频数直方图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)将频数直方图补充完整;
(3)如果该校九年级共有女生360人,估计仰卧起坐能够一分钟完成30次或30次以上的女学生有多少人?
(4)已知第一组有两名甲班学生,第四组中只有一名乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
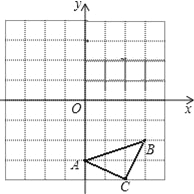
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有红色和蓝色两个布袋,红色布袋中有三个除标号外完全相同的小球,小球上分别标有数字1,2,3,蓝色布袋中有也三个除标号外完全相同的小球,小球上分别标有数字2,3,4小明先从红布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从蓝布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)用列表法或树状图表示出两次取得的小球上所标数字的所有可能结果;
(2)若把m、n分别作为点A的横坐标和纵坐标,求点A(m,n)在函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )

A. B.
B. C.
C.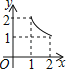 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】县政府计划建设一项水利工程,工程需要运送的土石方总量为![]() (单位:
(单位:![]() ),某运输公司承担了运送土石方的任务.
),某运输公司承担了运送土石方的任务.
(1)运输公司平均运输速度v(单位:![]() 天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
天)与完成运输所需时间t(单位:天)之间具有怎样的函数关系?
(2)这个运输公司共有80辆卡车,每天可运输土石方为![]() (单位:
(单位:![]() ),公司完成全部运输任务需要多长时间?
),公司完成全部运输任务需要多长时间?
(3)当公司以问题(2)中的速度工作了30天后,由于工程进度的需要,剩下的运输任务必须在20天内完成,则运输公司至少要增加多少辆卡车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在点Pk(xk,yk)处,其中x1=1,y1=2,当k≥2时,xk=xk﹣1+1﹣5([![]() ]﹣[
]﹣[![]() ]),yk=yk﹣1+[
]),yk=yk﹣1+[![]() ]﹣[
]﹣[![]() ],[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2017棵树种植点的坐标为( )
],[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0.按此方案,第2017棵树种植点的坐标为( )
A.(5,2017)B.(6,2016)C.(1,404)D.(2,404)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com