若m+n＝2.mn＝-5.则+＝ [ ] A．B． C．D．题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：初中数学 来源： 题型：

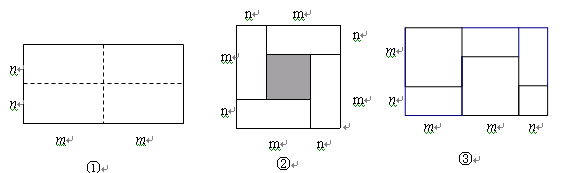
图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形

1.图②中的阴影部分的面积为；

2.观察图②请你写出三个代数式（m＋n）²、（m－n）²、mn之间的等量关系是

．

3.若x＋y＝5，xy＝2，则（x－y）²＝．

4.实际上有许多代数恒等式可以用图形的面积来表示．

如图③，它表示了．

5.试画出一个几何图形，使它的面积能表示（2m＋n）（m＋2n）＝2m²＋5mn＋2n²．

（此题6分）

查看答案和解析>>

科目：初中数学 来源： 题型：

数学课堂上，徐老师出示一道试题：
如图（十）所示，在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠ACP的平分线上一点．若∠AMN＝60°，求证：AM＝MN．
(1)经过思考，小明展示了一种正确的证明过程．请你将证明过程补充完整．
证明：在AB上截取EA＝MC，连结EM，得△AEM．
∵∠1＝180°－∠AMB－∠AMN，∠2＝180°－∠AMB－∠B，∠AMN＝∠B＝60°，∴∠1＝∠2．
又CN平分∠ACP，∠4＝∠ACP＝60°．∴∠MCN＝∠3＋∠4＝120°…………①
又∵BA＝BC，EA＝MC，∴BA－EA＝BC－MC，即BE＝BM．
∴△BEM为等边三角形．∴∠6＝60°．
∴∠5＝180°－∠6＝120°．………②
∴由①②得∠MCN＝∠5．
在△AEM和△MCN中，
∵
∴△AEM≌△MCN (ASA)．∴AM＝MN．
(2)若将试题中的“正三角形ABC”改为“正方形A₁B₁C₁D₁”（如图），N₁是∠D₁C₁P₁的平分线上一点，则当∠A₁M₁N₁＝90°时，结论A₁M₁＝M₁N₁．是否还成立？（直接写出答案，不需要证明）
(3) 若将题中的“正三角形ABC”改为“正多边形A_nB_nC_nD_n…X_n”，请你猜想：当∠A_nM_nN_n＝ °时，结论A_nM_n＝M_nN_n仍然成立？（直接写出答案，不需要证明）

查看答案和解析>>

科目：初中数学 来源： 题型：

图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形
【小题1】图②中的阴影部分的面积为                                         ；
【小题2】观察图②请你写出三个代数式（m＋n）²、（m－n）²、mn之间的等量关系是
                          ．
【小题3】若x＋y＝5，xy＝2，则（x－y）²＝         ．
【小题4】实际上有许多代数恒等式可以用图形的面积来表示．
如图③，它表示了                                         ．

【小题5】试画出一个几何图形，使它的面积能表示（2m＋n）（m＋2n）＝2m²＋5mn＋2n²．
（此题6分）

查看答案和解析>>

科目：初中数学 来源：2011-2012学年江苏江阴青阳中学七年级下学期期中数学试卷（带解析） 题型：解答题

图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形
【小题1】图②中的阴影部分的面积为                                         ；
【小题2】观察图②请你写出三个代数式（m＋n）²、（m－n）²、mn之间的等量关系是
                          ．
【小题3】若x＋y＝5，xy＝2，则（x－y）²＝         ．
【小题4】实际上有许多代数恒等式可以用图形的面积来表示．
如图③，它表示了                                         ．

【小题5】试画出一个几何图形，使它的面积能表示（2m＋n）（m＋2n）＝2m²＋5mn＋2n²．
（此题6分）

查看答案和解析>>

练习册

高中

初中

小学