
分析 (1)把原方程中的(x2-x)代换成y,即可得到关于y的方程,解之得到y的值,再分别求解关于x的方程即可得;
(2)设x2-3x=y,得到关于y的方程,解之得到y的值,再分别解关于x的方程即可;
(3)设x2+3x=y,得到关于y的方程,解之得到y的值,再分别解关于x的方程即可.
解答 解:(1)设x2-x=y,则原方程可化为:y2-5y-6=0,解得:y=-1或y=6,
当y=-1时,x2-x=-1,即x2-x+1=0,由△=(-1)2-4×1×1=-3<0知方程无解;
当y=6时,x2-x=6,即x2-x-6=0,由(x+2)(x-3)=0得x1=-2、x2=3;
(2)设x2-3x=y,则原方程可化为2y-$\frac{6}{y}$=-1,
整理得:2y2+y-6=0,即(y+2)(2y-3)=0,
解得:y=-2或y=$\frac{3}{2}$;
当y=-2时,x2-3x=-2,即x2-3x+2=0,由(x-1)(x-2)=0,解得:x=1或x=2;
当y=$\frac{3}{2}$时,x2-3x=$\frac{3}{2}$,即2x2-6x-3=0,解得:x=$\frac{3±\sqrt{15}}{2}$.
(3)设x2+3x=y,则原方程可化为$\sqrt{2y+1}$-y+7=0,
整理,得:y2-16y+48=0,
解得:y=4或y=12,
当y=4时,x2+3x=4,解得:x=1或x=-4;
当y=12时,x2+3x=12,解得:x=$\frac{-3±\sqrt{57}}{2}$.
点评 本题主要考查换元法在解一元二次方程中的应用.换元法是借助引进辅助元素,将问题进行转化的一种解题方法.这种方法在解题过程中,把某个式子看作一个整体,用一个字母去代表它,实行等量替换.这样做,常能使问题化繁为简,化难为易,形象直观.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | -a<-b | C. | -2a>-2b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.
如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
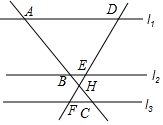 如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )
如图,直线l1∥l2∥l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,如果AB=5,BH=1,CH=2,那么$\frac{EF}{DE}$的值等于( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
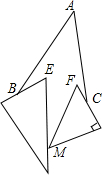 如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度.
如图,已知两块三角板如图摆放,点B和点C分别在两块三角板的边上,一块三角板的顶点M在另一块三角板的边上,且∠BAC=40°,∠E=60°,∠F=45°,则∠ABE+∠EMF+∠FCA=65 度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
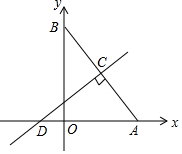 已知两直线l1:y1=k1x+b1,l2:y2=k2x+b2,若l1⊥l2,则有k1•k2=-1.
已知两直线l1:y1=k1x+b1,l2:y2=k2x+b2,若l1⊥l2,则有k1•k2=-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
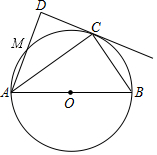 如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com