
”¾ĢāÄæ”æŌŚŅ»Ģõ±ŹÖ±µÄ¹«Ā·ÉĻÓŠA”¢B”¢CČżµŲ£¬AµŲŌŚB”¢CĮ½µŲÖ®¼ä£®¼×”¢ŅŅĮ½Į¾Ęū³µ·Ö±š“ÓB”¢CĮ½µŲĶ¬Ź±³ö·¢£¬ŃŲÕāĢõ¹«Ā·ŌČĖŁĻąĻņŠŠŹ»£¬¼×ŌČĖŁŠŠŹ»1Š”Ź±µ½“ļAµŲŗó¼ĢŠųŅŌĻąĶ¬µÄĖŁ¶ČĻņC“¦ŠŠŹ»£¬µ½“ļCŗóĶ£Ö¹£¬ŅŅŌČĖŁŠŠŹ»1.2Š”Ź±ŗ󵽓ļAµŲ²¢Ķ£Ö¹ŌĖ¶Æ£¬¼×”¢ŅŅĮ½³µĄėAµŲµÄ¾ąĄėy1”¢y2£ØĒ§Ć×£©ÓėŠŠŹ»Ź±¼äx£ØŹ±£©µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
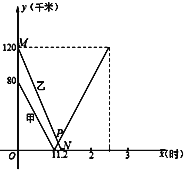
(1)BCµÄ¾ąĄėĪŖ km
¢ĘĒóĻ߶ĪMNµÄŗÆŹż±ķ“ļŹ½£»
¢ĒĒóµćPµÄ×ų±ź£¬²¢ĖµĆ÷µćPµÄŹµ¼ŹŅāŅ壻
¢Č³ö·¢¶ą³¤Ź±¼äŗ󣬼ה¢ŅŅĻą¾ą60km£æ
”¾“š°ø”æ£Ø1£©200£»£Ø2£©y=-100x+120£»£Ø3£©![]() £»(4)
£»(4) ![]() .
.
”¾½āĪö”æ
£Ø1£©¹Ū²ģĶ¼Ļó¼“æÉµĆ³öBCµÄ¾ąĄė£»
£Ø2£©øł¾ŻŗÆŹżĶ¼ĻóÖŠµÄŹż¾ŻæÉŅŌĒóµĆĻ߶ĪMNµÄŗÆŹż±ķ“ļŹ½£»
£Ø3£©øł¾ŻĢāŅāŗĶŗÆŹżĶ¼ĻóÖŠµÄŹż¾ŻæÉŅŌĒóµĆµćPµÄ×ų±ź£¬²¢ĖµĆ÷µćPµÄŹµ¼ŹŅāŅ壻
£Ø4£©·ÖŅŅ³µµ½“ļAµŲÖ®Ē°Ļą¾ą60kmŗĶµ½“ļAµŲÖ®ŗóĻą¾ą60kmĒó½ā£®
£Ø1£©ÓÉĶ¼Ļó¼“æÉµĆ³öBCµÄ¾ąĄėĪŖ80+120=200km£¬
¹Ź“š°øĪŖ£ŗ200£»
£Ø2£©ÉčĻ߶ĪMNµÄŗÆŹż±ķ“ļŹ½ĪŖy=kx+b£¬
![]() £¬½āµĆ
£¬½āµĆ![]() £¬
£¬
¼“Ļ߶ĪMNµÄŗÆŹż±ķ“ļŹ½ĪŖy=-100x+120£»
£Ø2£©”ßv¼×=80”Ā1=80£¬vŅŅ=120”Ā1.2=100£¬
”ą£Ø120+80£©”Ā£Ø100+80£©=![]() £¬
£¬
°Ńx=![]() “śČėy=-100x+120£¬µĆy=
“śČėy=-100x+120£¬µĆy=![]() £¬
£¬
”ąµćPµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£¬
£©£¬
µćPµÄŹµ¼ŹŅāŅå±ķŹ¾ŠŠŹ»ĮĖ![]() Š”Ź±ŗ󣬼ה¢ŅŅĮ½³µĻąÓö£¬“ĖŹ±ĄėAµŲµÄ¾ąĄėĪŖ
Š”Ź±ŗ󣬼ה¢ŅŅĮ½³µĻąÓö£¬“ĖŹ±ĄėAµŲµÄ¾ąĄėĪŖ![]() Ē§Ć×£»
Ē§Ć×£»
£Ø4£©Éč³ö·¢xŠ”Ź±ŗ󣬼ה¢ŅŅĻą¾ą60km£¬
·ÖĮ½ÖÖĒéæö£ŗ
¢ŁŅŅ³µµ½“ļAµŲÖ®Ē°¾ąĄėĪŖ60 km£¬ÓÉĢāŅāµĆ£Ø80+100£©x+60=200£¬
½āµĆx=![]() £»
£»
¢ŁŅŅ³µµ½“ļAµŲÖ®ŗó¾ąĄėĪŖ60 km£¬ÓÉĢāŅāµĆ80x=80+60£¬
½āµĆx=![]() £¬
£¬
ĖłŅŌ³ö·¢![]() »ņ
»ņ![]() Š”Ź±ŗ󣬼ה¢ŅŅĻą¾ą60km.
Š”Ź±ŗ󣬼ה¢ŅŅĻą¾ą60km.


 æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø
æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø
æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø Ņ»æĪŅ»Į·Ņ»±¾ĶØĻµĮŠ“š°ø
Ņ»æĪŅ»Į·Ņ»±¾ĶØĻµĮŠ“š°ø Õć½Ö®ŠĒѧŅµĖ®Ę½²āŹŌĻµĮŠ“š°ø
Õć½Ö®ŠĒѧŅµĖ®Ę½²āŹŌĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠÓŠČżøöµćA£Ø1£¬©1£©”¢B£Ø©1£¬©1£©”¢C£Ø0£¬1£©£¬µćP£Ø0£¬2£©¹ŲÓŚAµÄ¶Ō³ĘµćĪŖP1£¬P1¹ŲÓŚBµÄ¶Ō³ĘµćĪŖP2£¬P2¹ŲÓŚCµÄ¶Ō³ĘµćĪŖP3£¬°““Ė¹ęĀɼĢŠųŅŌA”¢B”¢CĪŖ¶Ō³ĘÖŠŠÄÖŲø“Ē°ĆęµÄ²Ł×÷£¬ŅĄ“ĪµĆµ½P4”¢P5”¢P6£¬”£¬ŌņµćP2018µÄ×ų±źŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
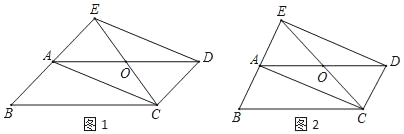
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬µćOŹĒ±ßADµÄÖŠµć£¬Į¬½ÓCO²¢ŃÓ³¤½»BAŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓED”¢AC£®
£Ø1£©ČēĶ¼1£¬ĒóÖ¤£ŗĖıߊĪAEDCŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČēĶ¼2£¬ČōĖıߊĪAEDCŹĒ¾ŲŠĪ£¬ĒėĢ½¾æ”ĻCODÓė”ĻBµÄŹżĮæ¹ŲĻµ£¬Š“³öÄćµÄĢ½¾æ½įĀŪ£¬²¢¼ÓŅŌÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
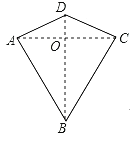
”¾ĢāÄæ”æĮ½×éĮŚ±ßĻąµČµÄĖıߊĪ½Š×ö”°óŻŠĪ”±£¬ČēĶ¼£¬ĖıߊĪABCDŹĒŅ»øöóŻŠĪ£¬ĘäÖŠ AB=CB,AD=CD,ղķĖ¹ŌŚĢ½¾æóŻŠĪµÄŠŌÖŹŹ±£¬µĆµ½ČēĻĀ½įĀŪ£ŗ¢Ł ACBD£»¢ŚAOCO![]() AC£»¢Ū”÷ABD”Õ”÷CBD£»¢ÜĖıߊĪABCDµÄĆ껿=
AC£»¢Ū”÷ABD”Õ”÷CBD£»¢ÜĖıߊĪABCDµÄĆ껿=![]() ACBD£¬ĘäÖŠ£¬ÕżČ·µÄ½įĀŪÓŠ_____.
ACBD£¬ĘäÖŠ£¬ÕżČ·µÄ½įĀŪÓŠ_____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
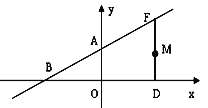
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼Ļó½»yÖįÓŚµćA£¬½»xÖįÓŚµćB£¬µćFŌŚÉäĻßBAÉĻ£¬¹żµćF×÷xÖįµÄ“¹Ļߣ¬µćDĪŖ“¹×ć£¬
µÄĶ¼Ļó½»yÖįÓŚµćA£¬½»xÖįÓŚµćB£¬µćFŌŚÉäĻßBAÉĻ£¬¹żµćF×÷xÖįµÄ“¹Ļߣ¬µćDĪŖ“¹×ć£¬
¢ÅČōOD=6£¬ĒóFµćµÄ×ų±ź£»
(2)ČōOD=12£¬MŌŚĻ߶ĪFDÉĻ£¬MµÄׯ×ų±źĪŖm£¬Į¬½ÓBM£¬ÓĆŗ¬ÓŠmµÄ“śŹżŹ½±ķŹ¾”÷BMFµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ŃOµÄÖ±¾¶AB=12£¬ĻŅAC=10£¬DŹĒ ![]() µÄÖŠµć£¬¹żµćD×÷DE”ĶAC£¬½»ACµÄŃÓ³¤ĻßÓŚµćE.
µÄÖŠµć£¬¹żµćD×÷DE”ĶAC£¬½»ACµÄŃÓ³¤ĻßÓŚµćE. 
£Ø1£©ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©ĒóAEµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬AB”ĪCD”ĪEF£¬BC”ĪAD£¬ACĘ½·Ö”ĻBADĒŅÓėEF½»ÓŚµćO£¬ÄĒĆ“Ķ¼ÖŠÓė”ĻAOEĻąµČµÄ½ĒÓŠ(””””)

A. 3øö B. 4øö C. 5øö D. 6øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĶ¬Ń§ŌŚĘ½Ź±µÄĮ·Ļ°ÖŠ£¬Óöµ½ĻĀĆęŅ»µĄĢāÄæ£ŗ
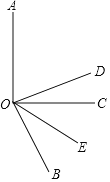
ČēĶ¼£¬”ĻAOC=90”ć£¬OE Ę½·Ö”ĻBOC£¬ODĘ½·Ö”ĻAOB.
¢ŁČō”ĻBOC=60”ć£¬Ēó”ĻDOE ¶ČŹż£»
¢ŚČō”ĻBOC=¦Į£Ø0£¼¦Į£¼90”ć£©£¬ĘäĖūĢõ¼ž²»±ä£¬Ēó”ĻDOE µÄ¶ČŹż.
£Ø1£©ĻĀĆęŹĒijĶ¬Ń§¶Ō¢ŁĪŹµÄ²æ·Ö½ā“š¹ż³Ģ£¬ĒėÄć²¹³äĶźÕū.
”ßOE Ę½·Ö”ĻBOC£¬”ĻBOC=60”ć
”ą”ĻBOE= . (½ĒĘ½·ÖĻߵĶØŅå)
”ß”ĻAOC=90”ć£¬”ĻBOC=60”ć
”ą £¬
”ßOD Ę½·Ö”ĻAOB£¬
”ą £¬(½ĒĘ½·ÖĻߵĶØŅå)
”ą”ĻDOE= .
£Ø×¢£ŗ·ūŗŔ߱ķŹ¾ŅņĪŖ£¬ÓĆ·ūŗÅ”ą±ķŹ¾ĖłŅŌ£©.
£Ø2£©·ĀÕÕ¢ŁµÄ½ā“š¹ż³Ģ£¬Ķź³ÉµŚ¢ŚŠ”Ģā.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ŃĻĀĮŠø÷ŹżĢīŌŚĻąÓ¦µÄ“óĄØŗÅĄļ£Ø½«ø÷ŹżÓƶŗŗÅ·ÖæŖ£©£ŗ©4£¬0.62£¬ ![]() £¬18£¬0£¬©8.91£¬+100
£¬18£¬0£¬©8.91£¬+100
ÕżŹż£ŗ{______”};øŗŹż£ŗ{______”};ÕūŹż£ŗ{______”};·ÖŹż£ŗ{______”}.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com