
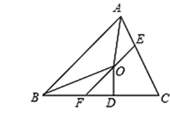
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F,交AC于点E,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=
∠C;②AE+BF=EF;③当∠C=90°时,E、F分别是AC、BC的中点;④若OD=![]() CE+CF=
CE+CF=![]() 则S△CEF=
则S△CEF=![]() ,其中正确的是______________
,其中正确的是______________
【答案】①②④
【解析】
根据三角形的内角和定理可得∠BAC+∠ABC=180°-∠C,再根据角平分线的定义可得∠OAB+∠OBA=![]() (∠BAC+∠ABC),然后根据三角形的内角和定理列式整理即可得解,判断出①正确;由平行线的性质和角平分线的定义得出△BFO和△AEO是等腰三角形得出AE+BF=EF故②正确;根据角平分线的定义判断出点O在∠ACB的平分线上,从而得到点O不是∠ACB的平分线的中点,然后判断出③错误;根据角平分线上的点到角的两边距离相等可得点O到AC的距离等于OD,再利用三角形的面积公式列式计算即可得到S△CEF=ab,判断出④正确.
(∠BAC+∠ABC),然后根据三角形的内角和定理列式整理即可得解,判断出①正确;由平行线的性质和角平分线的定义得出△BFO和△AEO是等腰三角形得出AE+BF=EF故②正确;根据角平分线的定义判断出点O在∠ACB的平分线上,从而得到点O不是∠ACB的平分线的中点,然后判断出③错误;根据角平分线上的点到角的两边距离相等可得点O到AC的距离等于OD,再利用三角形的面积公式列式计算即可得到S△CEF=ab,判断出④正确.
在△ABC中,∠BAC+∠ABC=180°-∠C,
∵∠BAC和∠ABC的平分线相交于点O,
∴∠OAB+∠OBA=![]() (∠BAC+∠ABC)=90°-
(∠BAC+∠ABC)=90°-![]() ∠C,
∠C,
在△AOB中,∠AOB=180°-(90°-![]() ∠C)=90°+
∠C)=90°+![]() ∠C,故①正确;
∠C,故①正确;
∵在△ABC中,∠BAC和∠ABC的平分线相交于点O,
∴∠OBC=∠OBA,∠OAE=∠OAB,
∵EF∥AB,
∴∠OBA=∠BOF,∠BAO=∠AOE,
∴∠BOF=∠FBO,∠OAE=∠AOE,
∴FB=FO,EO=EA,
∴EF=OE+OF=BF+AE,
故②正确;
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠ACB的平分线上,
∴点O不是∠ACB的平分线的中点,
∵EF∥AB,
∴E,F一定不是AC,BC的中点,故③错误;
∵点O在∠ACB的平分线上,
∴点O到AC的距离等于OD,
∴S△CEF=![]() (CE+CF)OD=
(CE+CF)OD=![]() ×2ba=ab,故④正确;
×2ba=ab,故④正确;
综上所述,正确的是①②④
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
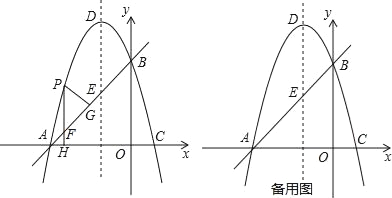
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD的面积为100,P为边CD上的任一点,E,F分别为线段AP,BP的中点,则图中阴影部分的总面积为( )

A. 30B. 25C. 22.5D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华为手机新款上市,十分畅销.某经销商进价每台3000元,售价每台4000 元.一月份销量为512台,二、三月份销量持续走高,三月份销量达到800台.
(1)求二、三月份每月销量的平均增长率;
(2)根据市场调查经验,四月份此款手机销售情况将不再火爆而是趋于平稳.若售价不变,四月份销量将与三月份持平;若降价促销,每台每降价50元,月销量将增加100台.要使四月份利润达到90万元,每台应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了决定谁将获得仅有的一张科普报告入场劵,甲和乙设计了如下的摸球游戏:在不透明的A、B两个口袋中分别放入编号分别为1,2,3的三个红球及一个白球,四个小球除了颜色和编号不同外,其他没有任何区别;甲在A口袋中摸出两个球,乙在B口袋中摸出一个球,如果甲摸出的两个球都是红色的甲得1分,否则,甲得0分,如果乙摸出的球是白色的,乙得1分,否则乙得0分,得分高的获得入场券,如果得分相同,游戏重来.
(1)运用列表或画树状图的方法求甲得1分的概率;
(2)请你用所学的知识说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①![]() ;②点E到AB的距离是
;②点E到AB的距离是![]() ;③
;③![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
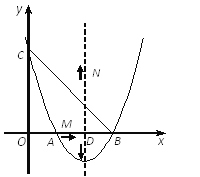
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
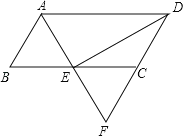
【题目】如图,在ABCD中,∠BAD的角平分线交BC于点E,交DC的延长线于点F,连接DE.
(1)求证:DA=DF;
(2)若∠ADE=∠CDE=30°,DE=2![]() ,求ABCD的面积.
,求ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com