【答案】
分析:(1)利用圆周角定理以及等腰三角形的性质求出∠BOP即可,再利用弧长公式求出n与t的关系即可;
(2)①当BP∥AC时,以及当PC∥AB时,分别利用等腰梯形的性质求出即可;
②以AB为腰时,以AB为底边时,再利用在△APC中,∠APC=60°,△APC是等边三角形和在△BPC中,∠BPC=105°,只有BP=PC这种情况,分别求出即可.
解答:解:(1)∵∠AOB=90°,∴∠BAO=45°,
∵∠BAC=75°,∴∠CAO=30°,
∵AO=CO,
∴∠CAO=∠OCA=30°,
∴∠AOC=180°-30°-30°=120°,
∴∠BOP=360°-90°-120°=150°,
∵∠BOP=n°,则
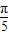
t=
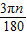
,整理得出:n=12t,
当n=150°时,150°=12t,t=12.5,故0≤t≤12.5.
(2)①∠BOP=n°,n=12t.
如图1,当BP∥AC时,t=5秒,四边形PBAC为等腰梯形.
理由:∵∠PBA=180°-75°=105°,
∵∠OBA=45°∴∠OBP=60°,OB=OP,
∴∠BOP=60°,则60=12t,
解得:t=5(秒),
又∵∠AOP=150°,∠ACP=75°,∴AB 与PC不平行.
又∵∠POC=150°-60°=90°=∠AOB,
∴AB=PC,∴四边形PBAC为等腰梯形.
如图2,当PC∥AB时,n=120=12t,解得:t=10(秒)
理由:∵∠CPB=180°-75°=105°,
∵∠OBA=45°,∴∠OBP=30°,OB=OP,
∴∠BOP=120°,则120=12t,
解得:t=10(秒),
又∵∠ACP=180°-75°=105°,∠BPC=105°,∴PB与AC不平行.
又∵∠POB=120°=∠AOC,
∴PB=AC,∴四边形PBAC为等腰梯形.
②在△ABP中,以AB为腰时(如图3),
∵∠BPA=∠BAP=45°,
∴∠BOP=45°+45°=90°,
故n=90=12t,解得:t=7.5(秒),
以AB为底边时(如图4),
∵∠BPA=

∠BOA=45°,∴∠BAP=67.5°,∴∠BOP=2×67.5°,
故135=12t,
解得:t=11.25(秒).
如图5.在△APC中,∠APC=60°,△APC是等边三角形,
∴∠BAP=15°,∠BOP=30°,
故30=12t,解得:t=2.5(秒).
如图6,在△BPC中,∠BPC=105°,只有BP=PC这种情况,
此时P是弧BC的中点,或说AP是∠BAC的平分线,
∠BOP=75°,
故n=75=12t,
解得:t=6.25(秒).
综合上述:当点P运动时间为5,10秒,四边形ABPC为等腰梯形;
当点P运动时间为7.5,11.25秒,三角形ABP为等腰三角形;
当点P运动时间为2.5秒,三角形APC为正三角形;
当点P运动时间为6.25秒,三角形BPC为等腰三角形.
点评:此题主要考查了圆的综合应用以及等腰梯形的判定和等腰三角形的性质以及弧长公式的应用等知识,利用数形结合以及分类讨论是解题关键.

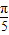 厘米/秒的速度在劣弧BC上运动,且运动时间为t(秒),∠AOB=90°、∠BOP=n°.
厘米/秒的速度在劣弧BC上运动,且运动时间为t(秒),∠AOB=90°、∠BOP=n°.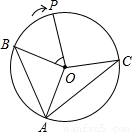
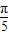 t=
t=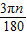 ,整理得出:n=12t,
,整理得出:n=12t,
 ∠BOA=45°,∴∠BAP=67.5°,∴∠BOP=2×67.5°,
∠BOA=45°,∴∠BAP=67.5°,∴∠BOP=2×67.5°,

 应用题作业本系列答案
应用题作业本系列答案
 速度在劣弧BC上运动,且运动时间为t(秒),∠AOB=90°、∠BOP=n°.
速度在劣弧BC上运动,且运动时间为t(秒),∠AOB=90°、∠BOP=n°.![]() 厘米的弦AB,则此弦所对的圆心角∠AOB为
厘米的弦AB,则此弦所对的圆心角∠AOB为