
如图,已知二次函数y=x -4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
(1) y=-x+3;(2) ( ,
,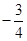 ).
).
解析试题分析:(1)利用y=x2-4x+3的图象交x轴于A、B两点(点A在点B的左侧),抛物线y=x2-4x+3交y轴于点C,即可得出A,B,C点的坐标,将B,C点的坐标分别代入y=kx+b(k≠0),即可得出解析式;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.
试题解析:(1)设直线BC的解析式为:y=kx+b(k≠0).
令x2-4x+3=0,
解得:x1=1,x2=3,
则A(1,0),B(3,0),C(0,3),
将B(3,0),C(0,3),代入y=kx+b(k≠0),得 ,
,
解得:k=-1,b=3,
BC所在直线为:y=-x+3;
(2)设过D点的直线与直线BC平行,且抛物线只有一个交点时,△BCD的面积最大.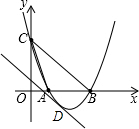
∵直线BC为y=-x+3,
∴设过D点的直线为y=-x+b,
∴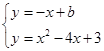 ,
,
∴x2-3x+3-b=0,
∴△=9-4(3-b)=0,
解得b= ,
,
∴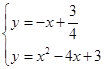 ,
,
解得,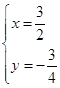 ,
,
则点D的坐标为:( ,
,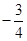 ).
).
考点: 1.抛物线与x轴的交点;2.待定系数法求一次函数解析式;3.二次函数图象上点的坐标特征.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
如图①,将□ABCD置于直角坐标系中,其中BC边在x轴上(B在C的左边),点D坐标为(0,4),直线MN: 沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
沿着x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被□ABCD截得的线段长度为m,平移时间为t,m与t的函数图像如图②所示.
(1)填空:点C的坐标为 ;
在平移过程中,该直线先经过B、D中的哪一点? ;(填“B”或“D”)
(2)点B的坐标为 ,n= ,a= ;
(3)求图②中线段EF的解析式;
(4)t为何值时,该直线平分□ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为鼓励居民节约用水,某市决定对居民用水收费实行“阶梯价”,即当每月用水量不超过15吨时(包括15吨),采用基本价收费;当每月用水量超过15吨时,超过部分每吨采用市场价收费,小兰家4、5月份的用水量及收费情况如下表:
| 月份 | 用水量(吨) | 水费(元) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
四川省第十二届运动会将于2014年8月18日在我市隆重开幕,根据大会组委会安排,某校接受了开幕式大型团体操表演任务.为此,学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.
(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;
(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
函数常用的表示方法有三种.
已知A、B两地相距30千米,小王以40千米/时的速度骑摩托车从A地出发匀速前往B地参加活动.请选择两种方法来表示小王与B地的距离y(千米)与行驶时间x(小时)之间的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
B岛位于自然环境优美的西沙群岛,盛产多种鱼类.A港、B岛、C港依次在同一条直线上,一渔船从A港出发经由B岛向C港航行,航行2小时时发现鱼群,于是渔船匀速缓慢向B港方向前行打渔.在渔船出发一小时后,一艘快艇由C港出发,经由B岛前往A港运送物资.当快艇到达B岛时渔船恰好打渔结束,渔船又以原速经由B岛到达C港.下面是两船距B港的距离y(海里)与渔船航行时间x(小时)的函数图象,结合图象回答下列问题:
(1)请直接写出m,a的值.
(2)求出线段MN的解析式,并写出自变量的取值范围.
(3)从渔船出发后第几小时两船相距10海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com