
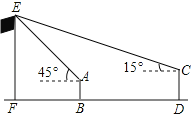
【题目】某校九(1)班开展数学活动,李明和张华两位同学合作用测角仪测量学校旗杆的高度,李明站在B点测得旗杆顶端E点的仰角为45°,张华站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知李明和张华相距(BD)30米,李明的身高(AB)1.6米,张华的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
【答案】旗杆的高![]() 为
为![]() 米.
米.
【解析】
过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.15m.由李明站在B点测得旗杆顶端E点的仰角为45°,可得△AEM是等腰直角三角形,继而得出得出AM=ME,设AM=ME=xm,则CN=(x+30)m,EN=(x-0.15)m.在Rt△CEN中,由tan∠ECN=![]() ,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.
,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF.
过点A作AM⊥EF于M,过点C作CN⊥EF于N,
∵AB=1.6,CD=1.75,
∴MN=0.15m,
∵∠EAM=45°,
∴AM=ME,
设AM=ME=xm,
则CN=(x+30)m,EN=(x-0.15)m,
∵∠ECN=15°,
∴tan∠ECN=![]() =
=![]() ,
,
即![]() ≈0.27,
≈0.27,
解得:x≈11.3,
则EF=EM+MF≈11.3+1.6=12.9(m),
答:旗杆的高![]() 为
为![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
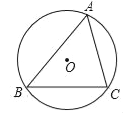
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
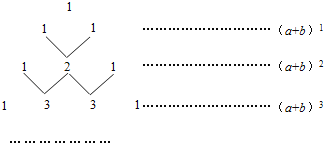
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的高作等腰三角形”的尺规作图的过程.
已知:如图1,线段a和线段b.
求作:△ABC,使得AB=AC,BC=a,BC边上的高为b.
作法:如图2,
①作射线BM,并在射线BM上截取BC=a;
②作线段BC的垂直平分线PQ,PQ交BC于D;
③以D为圆心,b为半径作圆,交PQ于A;
④连接AB和AC.
则△ABC就是所求作的图形.
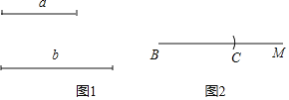
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:由作图可知BC=a,AD=b.
∵PQ为线段BC的垂直平分线,点A在PQ上,
∴AB=AC(______)(填依据).
又∵AD在线段BC的垂直平分线PQ上,
∴AD⊥BC.
∴AD为BC边上的高,且AD=b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的动点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax+dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图1,正方形ABCD的中心为点O,A(3,3).
①点O到线段AB的“和距离”d(O,线段AB)=______;
②设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一个动点,如果6![]() <d(M,线段AC)<6+3
<d(M,线段AC)<6+3![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
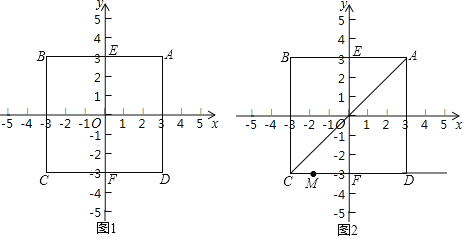
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为了节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费为更好地决策,自来水公司在某街道随机抽取了部分用户的用水量数据,按A,B,C,D,E五个区间进行统计,并将统计结果绘制如下两幅不完整的统计图,请你结合图中所给信息解答下列问题:(说明:A:0﹣3吨;B:3﹣6吨;C:6﹣9吨;D:9﹣12吨;E:12﹣16吨,且每组数据区间包括右端的数但不包括左端的数)
(1)这次随机抽样调查了_____用户
(2)补全频数分布直方图,求扇形统计图中B部分的圆心角的度数;
(3)如果自来水公司将基本用水量定为每户9吨,那么该街道1.8万用户中约有多少用户的用水全部享受基本用水量的价格?
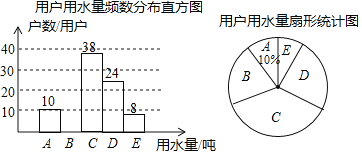
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产,已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为2.8万元,乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com