
分析 根据x1=2以及xk=xk-1+1-4([$\frac{k-1}{4}$]-[$\frac{k-2}{4}$]),找出部分xk的值,根据数的变化找出变化规律“x4n+1=2,x4n+2=3,x4n+3=4,x4n+4=5(n为自然数)”,依此规律即可得出结论.
解答 解:∵x1=2,且当k≥2 时,满足xk=xk-1+1-4([$\frac{k-1}{4}$]-[$\frac{k-2}{4}$]),
∴x2=3,x3=4,x4=5,x5=2,x6=3,
∴x4n+1=2,x4n+2=3,x4n+3=4,x4n+4=5(n为自然数).
∵2016=4×504,
∴x2016=x4=5.
故答案为:5.
点评 本题考查了规律型中数字的变化类,根据数列中数的变化找出变化规律“x4n+1=2,x4n+2=3,x4n+3=4,x4n+4=5(n为自然数)”是解题的关键.


科目:初中数学 来源: 题型:解答题
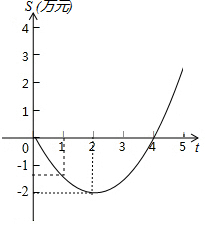 某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:
某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )
已知,直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰三角形Rt△ABC,∠BAC=90°,且点P(1,a)为坐标系中一个动点.要使得△ABC和△ABP的面积相等,则实数a的值( )| A. | a=4 | B. | a=±4 | C. | a=-3 | D. | a=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
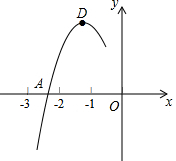 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根,其中正确结论的个数为3个.
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根,其中正确结论的个数为3个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1<k<-$\frac{1}{2}$ | B. | $\frac{1}{2}$<k<1 | C. | 0<k<1 | D. | 0<k<$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{5}$=$\frac{x}{4}$-10 | B. | $\frac{x}{5}$+$\frac{1}{6}$=$\frac{x}{4}$ | C. | 5x=4x+10 | D. | $\frac{x}{5}$-$\frac{x}{4}$=$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com