
阅读材料:(本题8分)
例:说明代数式  的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
解:  ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离,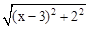 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,
只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
所以PA′+PB的最小值为线段A′B的长度.为此,构造直角
三角形A′CB,因为A′C=3,CB=3,所以A′B=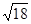 ,
,
即原式的最小值为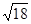 。
。
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
(2)求代数式  的最小值
的最小值
(1)B的坐标(2,3)或(2,-3)(2)10
解析试题分析:解:(1)B的坐标(2,3)或(2,-3)(填对一个就算对2分)
(2)∵原式化为 的形式,(2分)
的形式,(2分)
∴所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,7)、点B(6,1)
的距离之和。
如图所示:设点A关于x轴的对称点为A′,则PA=PA′,
∴求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B
间的直线段距离最短。 ∴PA′+PB的最小值为线段A′B的长度。
∵A(0,7),B(6,1),∴A′(0,-7),A′C=6,BC=8(2分)
∴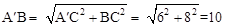 (2分)
(2分)
考点:本题考查了多边形的判定
点评:此类试题属于难度一般的试题,考生在解答此类试题时一定要对各多边形的基本判定熟练把握


科目:初中数学 来源: 题型:阅读理解
阅读材料,回答问题(本题满分12分)
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A向B以2cm/s的速度移动;点Q沿DA边从D向A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6),那么:
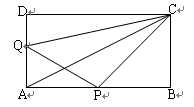
1.(1)当t为何值时,△QAP为等腰直角三角形?
2.(2)求四边形QAPC的面积;你有什么发现?
3.(3)当t为何值时,以点A、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源:2014届浙江省建德市八年级3月月考数学试卷(解析版) 题型:解答题
(本题8分)
阅读材料:如果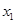 、
、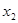 是一元二次方程
是一元二次方程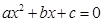 (
( ≠0)的两根,那么,
≠0)的两根,那么,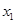 +
+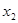 =
=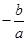 ,
,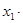
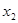 =
=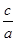 .这就是著名的韦达定理.
.这就是著名的韦达定理.
现在我们利用韦达定理解决问题:
已知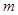 与
与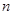 是方程
是方程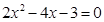 的两根,
的两根,
(1)填空: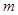 +
+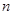 =________;
=________;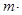
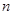 =________;
=________;
(2)计算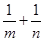 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省常州市七八年级上学期12月考数学试卷(解析版) 题型:解答题
阅读材料:(本题8分)
例:说明代数式  的几何意义,并求它的最小值.
的几何意义,并求它的最小值.
解:  ,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则
,如图,建立平面直角坐标系,点P(x,0)是x轴上一点,则 可以看成点P与点A(0,1)的距离,
可以看成点P与点A(0,1)的距离, 可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
可以看成点P与点B(3,2)的距离,所以原代数式的值可以看成线段PA与PB长度之和,它的最小值就是PA+PB的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,
只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
所以PA′+PB的最小值为线段A′B的长度.为此,构造直角
三角形A′CB,因为A′C=3,CB=3,所以A′B= ,
,
即原式的最小值为 。
。
根据以上阅读材料,解答下列问题:
(1)代数式 的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B 的距离之和.(填写点B的坐标)
(2)求代数式  的最小值
的最小值

查看答案和解析>>
科目:初中数学 来源:浙江省2013届八年级上学期期末考试数学卷 题型:选择题
(本题8分)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线L1,一次函数y=k2x+b2(k2≠0)的图象为直线L2,若k1=k2,且b1≠b2,我们就称直线L1与直线L2互相平行.解答下面的问题:
(1)求过点P(1,4),且与直线y=-2x-1平行的直线L的函数解析式,并画出直线L的图象;
(2)设直线L分别与y轴,x轴交于点A,B,如果直线m:y=kx+t(t>0)与直线L平行,且交x轴于点C,求出△ABC的面积S关于t函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com