
如图,直线 与双曲线
与双曲线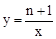 交于C、D两点,与x轴交于点A.
交于C、D两点,与x轴交于点A.
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S △ABC=4,求双曲线的解析式;
(3)在(1)、(2)的条件下,若AB= ,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
解:(1)由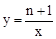 图象得:n+1<0,解得:n<-1。
图象得:n+1<0,解得:n<-1。
由y=kx+k,令y=0,解得: ,∴A坐标为(-1,0)。
,∴A坐标为(-1,0)。
(2)设C(a,b),
∵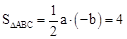 ,∴ab=-8。
,∴ab=-8。
∵点C在双曲线上,∴双曲线的解析式为 。
。
(3)∵CB⊥y轴,∴B(0,b)。
在Rt△AOB中,AB= ,OA=1,根据勾股定理得:OB=4。
,OA=1,根据勾股定理得:OB=4。
∴B(0,-4)。∴C(2,-4)。
将C代入直线y=kx+k中,得:2k+k=-4,即 。
。
∴直线AC解析式为 。
。
联立直线与反比例解析式得: ,解得:
,解得: 或
或 。
。
∴D(-3, )。
)。
则由图象可得:当x<-3或0<x<2时,反比例函数的值小于一次函数的值。
解析试题分析:(1)由反比例函数图象位于第二、四象限,得到比例系数小于0列出关于n的不等式,求出不等式的解集即可得到n的范围,对于直线解析式,令y=0求出x的值,确定出A的坐标即可。
(2)设C(a,b),表示出三角形ABC的面积,根据已知的面积列出关于a与b的关系式,利用反比例函数k的几何意义即可求出k的值,确定出反比例解析式。
(3)由CB垂直于y轴,得到B,C纵坐标相同,即B(0,b),在直角三角形AOB中,由AB与OA的长,利用勾股定理求出OB的长,确定出B坐标,进而确定出C坐标,将C代入直线解析式求出k的值,确定出一次函数解析式,与反比例解析式联立求出D的坐标,由C,D两点的横坐标,利用图象即可求出反比例函数的值小于一次函数的值时,自变量x的取值范围。


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
如图,一次函数y=-x+b与反比例函数 的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC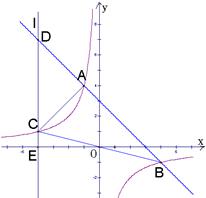
(1)、求出b和k;
(2)、求证:△ACD是等腰直角三角形;
(3)、在y轴上是否存在点P,使 ,若存在,请求出P的坐标,若不存在,请说明理由。
,若存在,请求出P的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,函数y1=-x+4的图象与函数y2= (x>0)的图象交于 A(a,1)、B(1,b)两点.
(x>0)的图象交于 A(a,1)、B(1,b)两点.
(1)求a,b及y2的函数关系式;
(2)观察图象,当x>0时,比较y1与y2大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,直线AB与
中,直线AB与 轴交于点A,与
轴交于点A,与 轴交于点C(
轴交于点C( ,
, ),且与反比例 函数
),且与反比例 函数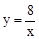 在第一象限内的图象交于点B,且BD⊥
在第一象限内的图象交于点B,且BD⊥ 轴于点D,OD
轴于点D,OD .
.
(1)求直线AB的函数解析式;
(2)设点P是 轴上的点,若△PBC的面积等于
轴上的点,若△PBC的面积等于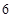 ,直接写出点P的坐标.
,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,双曲线 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的解析式;
(2)直接写出不等式 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xoy中,F是AB边上的动点(不与端点A、B重合),过点F的反比例函数 (k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(1)若S△OCF= ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与y轴的位置关系,并说明理由;
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).
(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
| A.两点确定一条直线 | B.垂线段最短 |
| C.两点之间线段最短 | D.三角形两边之和大于第三边 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com