
【题目】点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点间的距离表示为
两点间的距离表示为![]() .且
.且![]() .
.
(1)数轴上表示2和5的两点之间的距离是___,
数轴上表示2和5的两点之间的距离是___,
数轴上表示1和3的两点之间的距离是___;
(2)数轴上表示x和1的两点A和B之间的距离是___,如果|AB|=2,那么x=___;
(3)当代数式|x+1|+|x2|取最小值时,相应x的取值范围是___.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
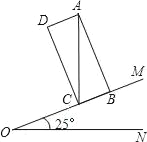
【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填空或填写适当的理由:
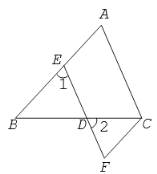
(1)![]() ,(已知)
,(已知)
![]() ______________.(___________________________________________)
______________.(___________________________________________)
![]() ________________
________________![]() (______________________________________)
(______________________________________)
(2)![]() _______,(已知)
_______,(已知)
![]() ;(___________________________________)
;(___________________________________)
(3)![]() _______________,(已知)
_______________,(已知)
![]() ___________
___________![]() _______________.(_______________________________)
_______________.(_______________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
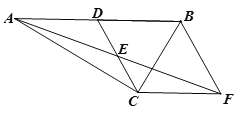
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=60°,求∠2、∠3的度数;
(2)若点![]() 是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系:
是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系:
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;请阅读下面的解答过程,并填空(理由或数学式).

解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB( )
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD( )
∴∠MPF=∠PFD( )
∴ =∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD.
②当点P在图3的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系: ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校![]() 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.

(1)![]() =________,
=________,![]() =_________;
=_________;
(2)请补全图中的条形图;
(3)在抽查的![]() 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC与Rt△ABD中,![]() ,
,![]() ,AC、BD相交于点G,过点A作
,AC、BD相交于点G,过点A作![]() 交CB的延长线于点E,过点B作
交CB的延长线于点E,过点B作![]() 交DA的延长线于点F,AE、BF相交于点H.
交DA的延长线于点F,AE、BF相交于点H.
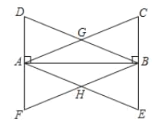
(1)证明:ΔABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com