
【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.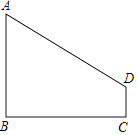
(1)求线段AD的长.
(2)在线段BC上是否存在点P,使△APD是等腰三角形?若存在,求出线段BP的长;若不存在,请说明理由.
【答案】
(1)解:如图1,过D作DE⊥AB于E点,

AE=4﹣1=3,DE=BC=4,
在Rt△AED中,AD= ![]() =5;
=5;
(2)解:如图2,

当AP=AD时,
在Rt△ABP中,BP= ![]() =3;
=3;
如图3,

当PA=PD时,
AB2+BP2=CD2+(BC﹣BP)2,即42+BP2=12+(4﹣BP)2,
解得BP= ![]() .
.
综上所述,线段BP的长是3或 ![]() .
.
【解析】(1)根据已知可知四边形ABCD是梯形,要解决梯形的问题通过作高,转化到直角三角形中解决。因此过D作DE⊥AB于E点,可证得BCDE是矩形,就可求出DE和AE的长,再根据勾股定理在Rt△AED中求出AD的长。
(2)根据题意可知,分两种情况,当AP=AD时,在Rt△ABP中,利用勾股定理求出BP的长;当PA=PD时,根据勾股定理,利用PA2=PD2,建立方程,求解即可。
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】若关于y的一元二次方程ky2﹣4y﹣3=3y+4有实根,则k的取值范围是( )
A.k>﹣ ![]()
B.k≥﹣ ![]() 且k≠0
且k≠0
C.k≥﹣ ![]()
D.k> ![]() 且k≠0
且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
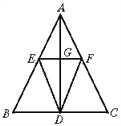
【题目】如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数y=(3﹣m)x+m﹣5.
(1)若一次函数的图象过原点,求实数m的值;
(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.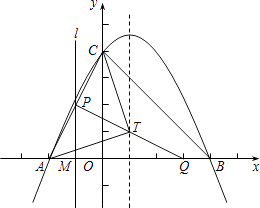
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 ![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com